Hi everyone! I’m currently writing this from a high rise hotel room in Boston. It’s my first time here but I haven’t been out to see the city yet because I can’t stop thinking about vectors.
In this post, we’ll talk about:
What is a vector?
Vector addition and scalar multiplication
Vectors in higher dimensions
What is a vector space?
A strange vector space
Transformations of vectors
This will be the first post in a short series covering the basics of linear algebra! I’m working my way through the book All The Math You Missed (But Need To Know for Graduate School) By Thomas A. Garrity because I want to review all my undergrad math.
1. What is a vector?
If linear algebra was a grand theatre, vectors would be the drag queens.
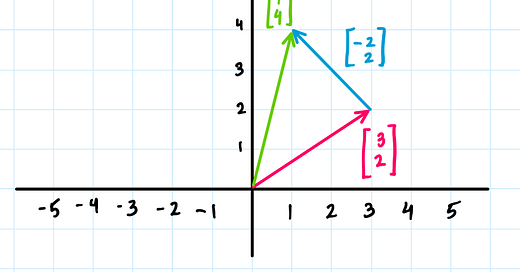
See, a vector has three identities. In drag, you get the visceral image of a vector as an arrow in space. Physics students may remember defining vectors as quantities that have magnitude and direction.
The magnitude is the length of the vector, and the direction is wherever the arrow is pointing. It can represent a gust of wind travelling at 10 metres per second blowing Northeast, or perhaps the path I took flying from Kansas City to Boston.
Under the glamour lives a more understated persona. Out of the spotlight, the vector is stripped down to its essential parts, which is simply a list of numbers.
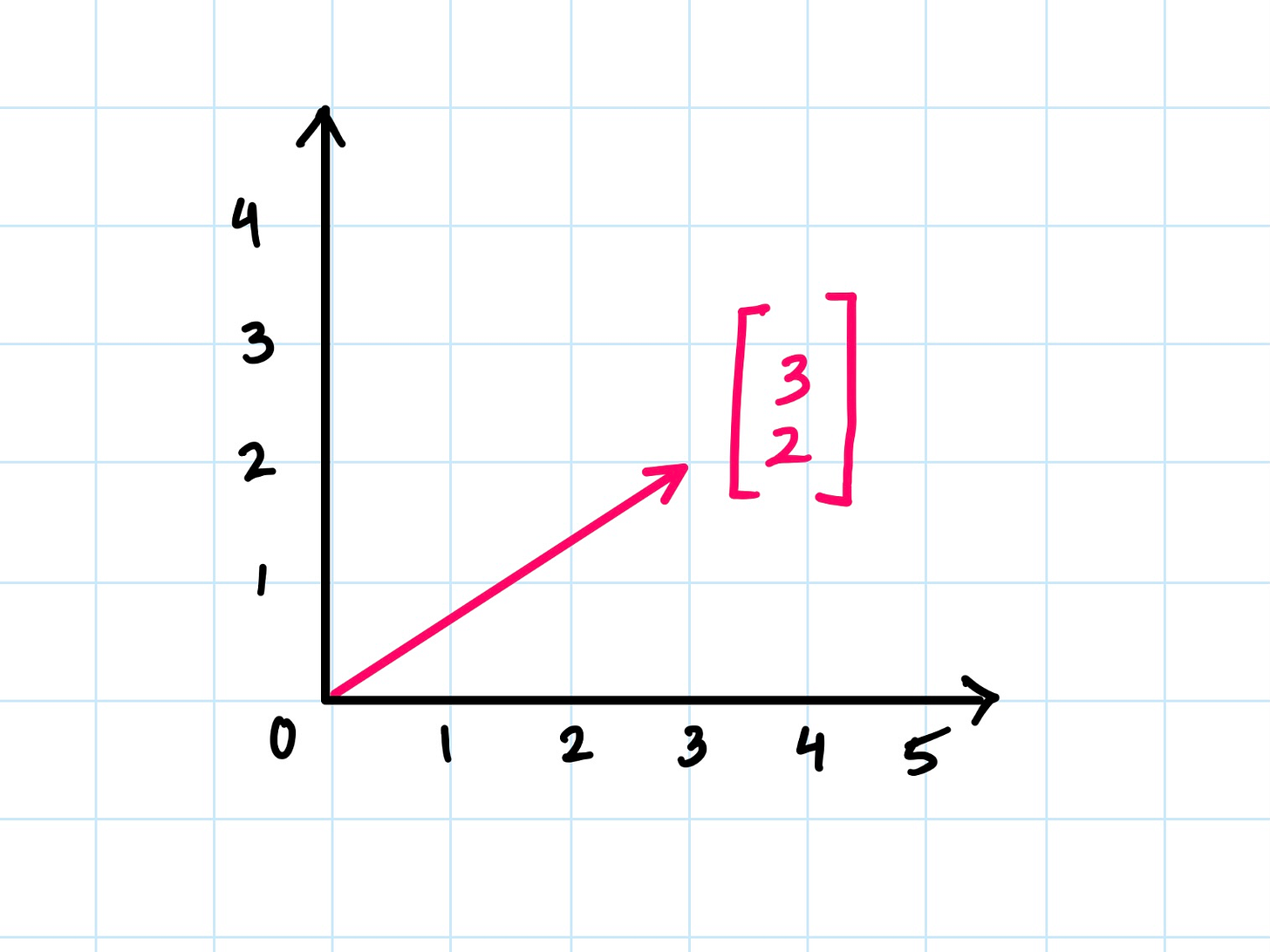
By placing the arrow in a coordinate system, we can define the vector by simply listing the coordinates of where the arrow points, when the vector starts at the origin.
In our example, the vector representing the pink arrow is the list [3, 2].
Vectors can be represented either as a column of numbers or as a row. For our purposes, we’ll think of these as representing the same idea, so if I switch between columns and rows, don’t worry about it.
This characterization might be more familiar to computer science students, who use vectors to store lists of data.
For example, if you’re taking 5 classes and your grades are 75, 80, 86, 92, and 89, you can store that information in a 5-dimensional vector:
In both characterizations, either as a geometric arrow or a numerical list, the order matters. Rearranging the numbers would move the arrow around, or mix up which grades came from which class.
There’s also a third, hidden side to every vector. The side that’s abstract, which no one sees, and few understand. This is how mathematicians often think about vectors: objects that permit addition and scalar multiplication.
2. Vector addition and scalar multiplication
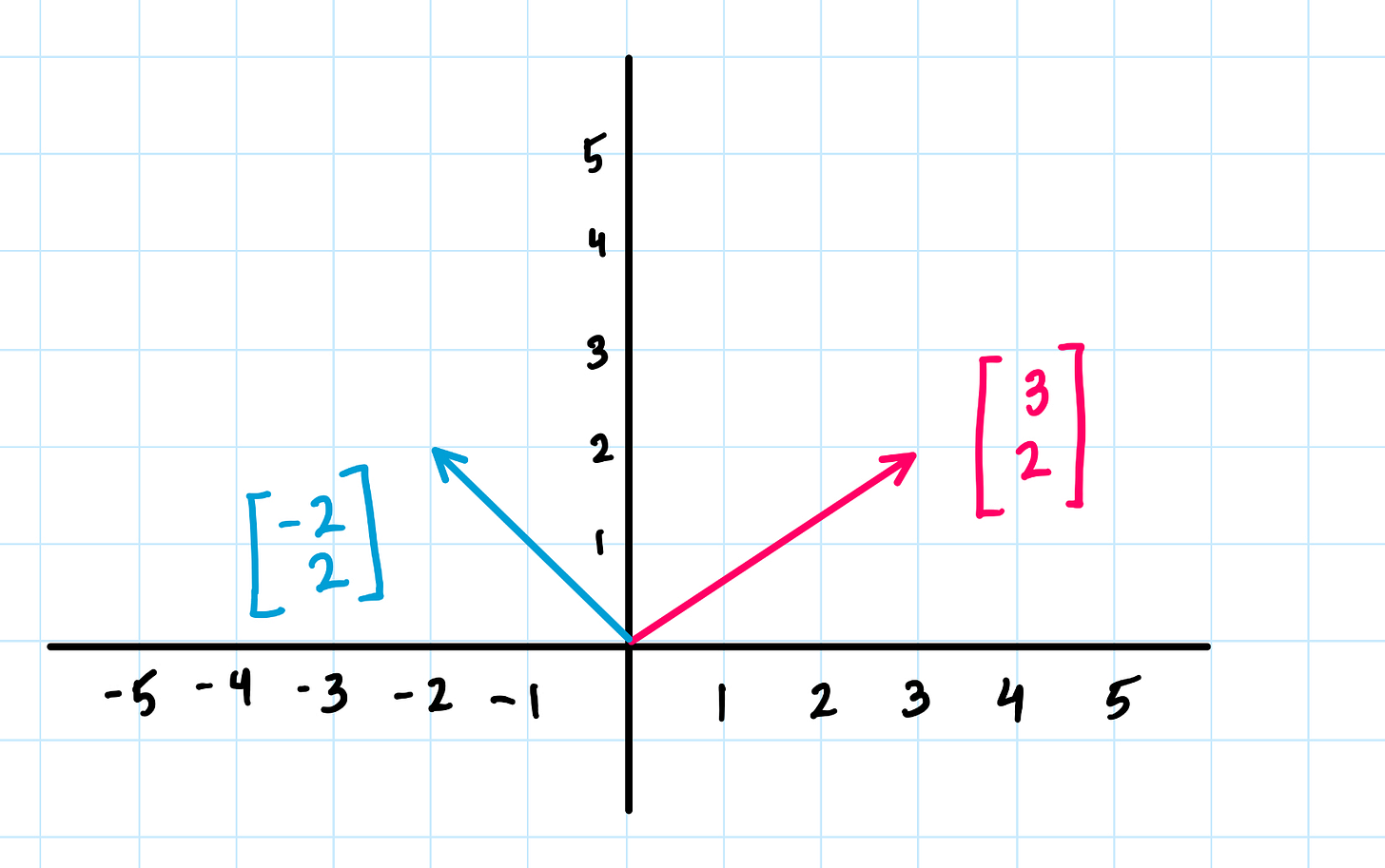
Let’s make sense of this with our previous two characterizations. Arrows in space can be added together by connecting them tip-to-tail, and then we define addition by just adding a third side to the triangle.
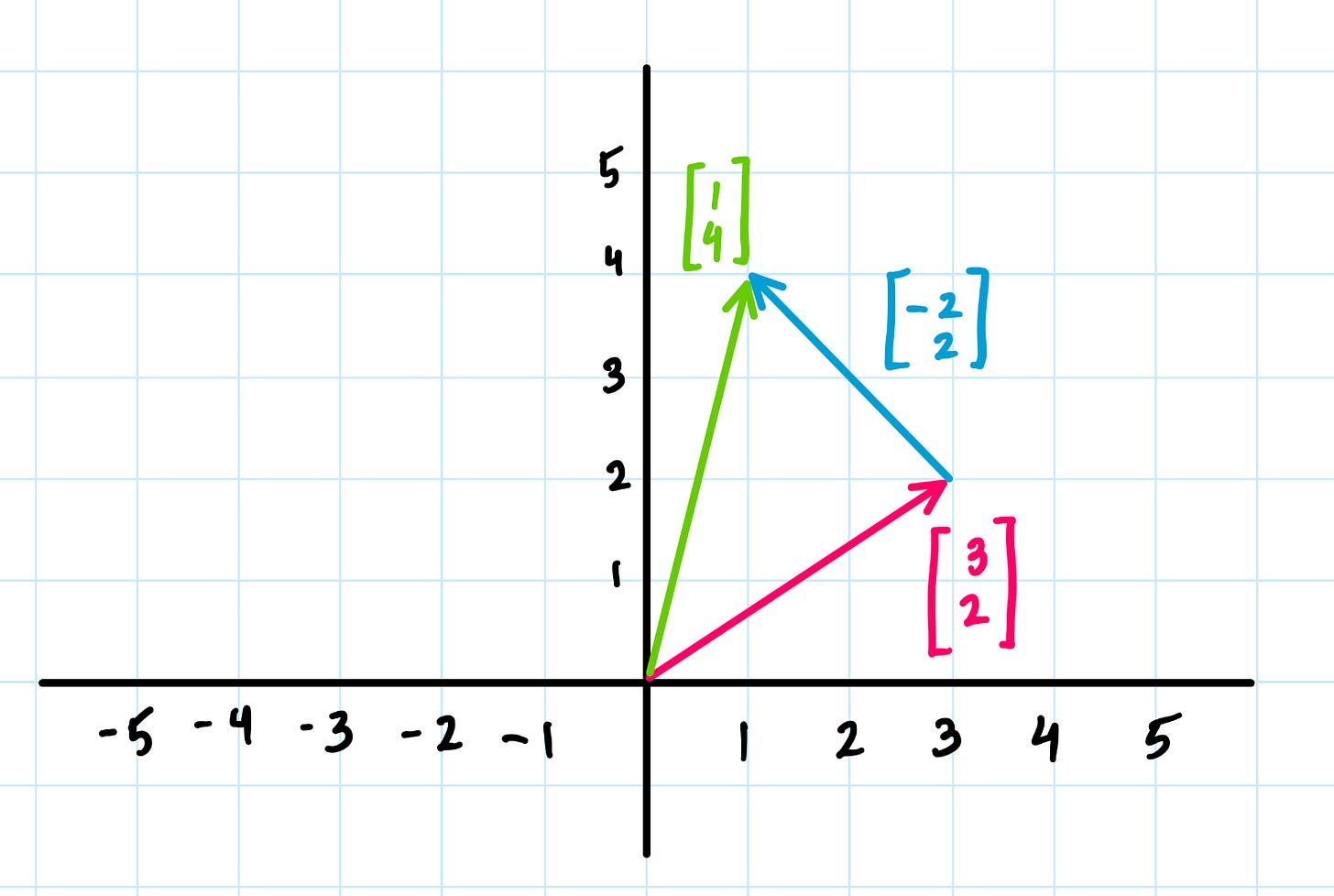
This agrees with our numerical definition of vectors. Since the coordinates of the pink and blue vectors are [3, 2] and [-2, 2], then adding them just means adding each coordinate. 3 + (-2) is 1, and 2 + 2 is 4, so the new vector has coordinates [1, 4].
From a physical perspective, you can think of this addition like a gust of wind blowing Northeast (the pink vector), meeting a gust of wind blowing Northwest (the blue vector). The Western and Eastern forces might balance each other out a bit, to make a gust that points more in the North direction.
Now what does “scalar multiplication” mean?
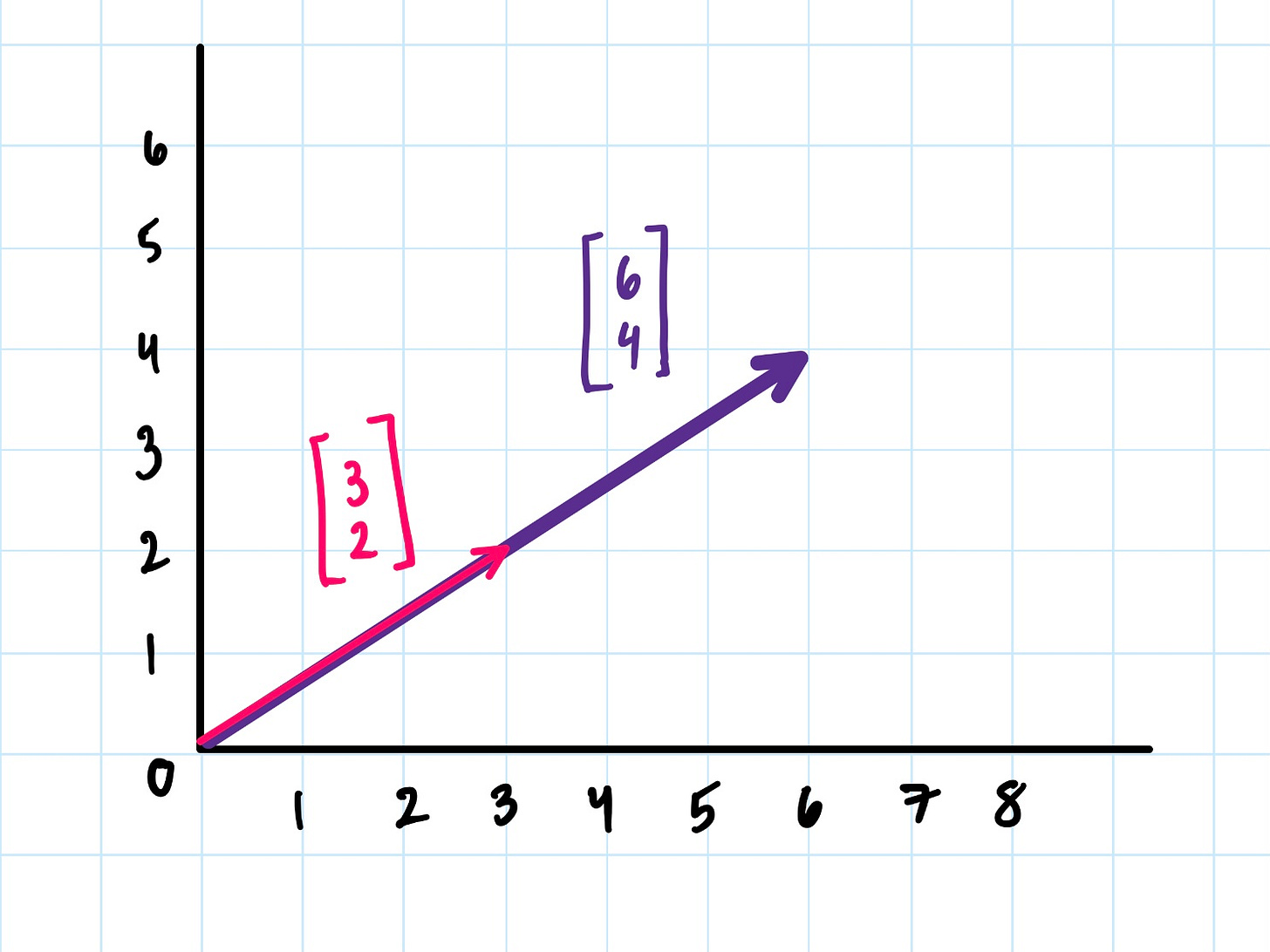
That just means we can scale the arrow by stretching it by some factor.
This is something we can view geometrically, like stretching the pink arrow into the purple arrow by doubling its length, or we can think of this numerically, by doubling the coordinates [3, 2] to get [6, 4].
3. Vectors in higher dimensions
The most typical vector space we’ll work with is called R2. Think of this like the Cartesian plane with an x-axis and y-axis. Each vector has 2 coordinates, which are both real numbers, hence, R2.
We can also work in R3, where a vector has 3 dimensions, x, y, and z.
Beyond 3 dimensions, it’s hard to visualize vectors geometrically. But there’s nothing stopping us from doing it algebraically!
Think about the 5-dimensional vector representing our grades in 5 classes:
This is a 5-dimensional vector, which you can’t visualize as an arrow, but you can still perform addition and scalar multiplications with it!
For example: taking the averages between your grades and your friends grades in the same classes involves both addition and scalar multiplication:
We can even do math with vectors in 1000 dimensions! They’re just large lists of numbers!
Even though it’s hard to visualize these higher dimensions with arrows and lines, the rules we set up in R2 and R3 can generalize neatly to any higher dimension, Rn (where n is any whole number).
4. What is a vector space?
R2, R3, and Rn are examples of vector spaces, which are just sets of vectors.
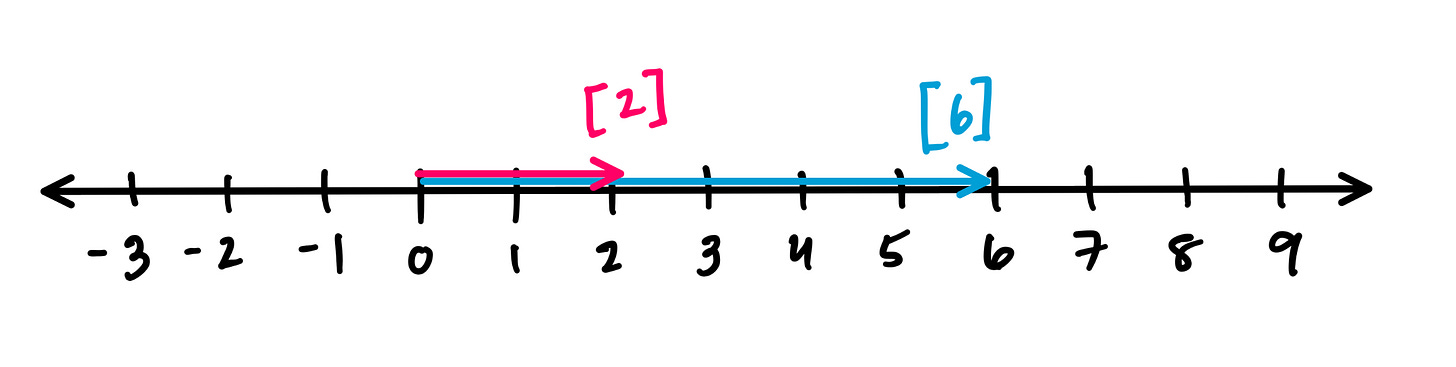
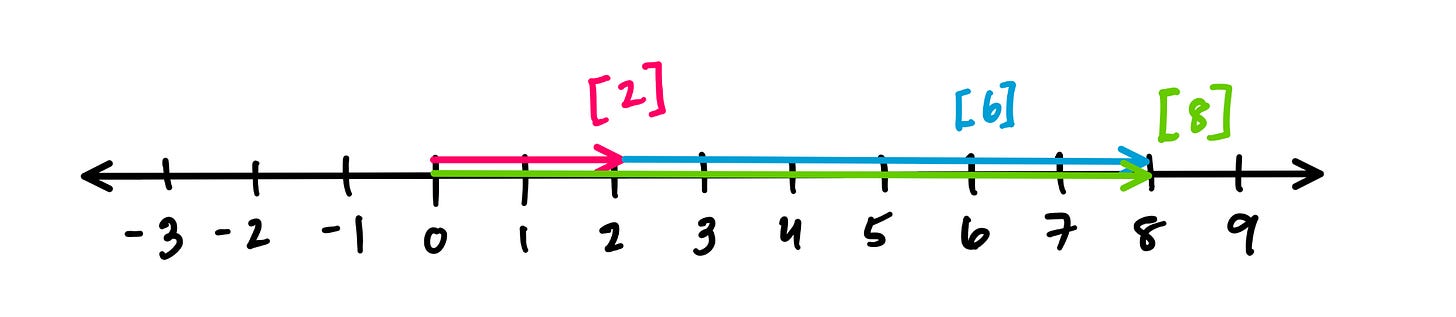
Perhaps the simplest vector space is the real number line R, where the vectors are simply numbers.
We can still visualize the number 2 as the arrow pointing from 0 (the origin) to the number 2, and we can “scale” this arrow by stretching it to the number 6. This corresponds to multiplying by 3.
We can also add these vectors tip-to-tail again, and adding 2+6 gives us 8, in green.
Remember when I said there was a third definition to a vector? One that was more abstract, and generalized to any object that we could add or scalar multiply. To get a better feeling of this, we’ll look at vector spaces.
A technical definition can be found here, but essentially, a vector space over the real numbers is a set with a well-defined notion of addition and scalar multiplication. By well-defined, I mean that these operations should work as expected:
You should be allowed to add some “zero” to a vector and get the same vector
You should be allowed to multiply a vector by 1 and get the same vector
Every vector should have an “additive inverse”, which you can add to it in order to get back to “zero”
The order of addition shouldn’t matter, just like how 1+2 is the same as 2+1.
Scalar multiplication should obey the distributive property, and follow the same rules as multiplication in the real numbers.
All of these conditions look pretty reasonable, right?
The elements of these vector spaces are what we call vectors.
5. A strange vector space
Aside from the traditional vector spaces, another example is the space of all polynomials with real coefficients up to degree 2.
Here are some examples of vectors in this space:
We can add two vectors in this space and get another vector:
And we can scalar multiply them:
Vectors don’t just have to look like arrows or lists. And this is the key idea I want to get across here.
Vectors can have multiple identities at the same time!
The goal of linear algebra is to draw connections between all these different identities vectors can have.
In particular, things we can do geometrically, like rotating or stretching a vector, correspond to mathematical operations on the list of numbers that the vector represents! And linear algebra is full of tools and definitions we can use to understand this relationship.
Playing with the visual, geometric side, can give us new insights on the numerical side, and vice versa.
6. Transformations of vectors
To give an example, imagine a picture where every pixel is represented by a vector. When we apply a transformation to the picture, it’s as if we’re stretching and manipulating the vectors! Look at what happens when I stretch this photo of me horizontally.
In this example, we’re stretching only the horizontal (x) component, while the vertical (y) component stays the same.
In both images, I’m about 10 squares tall, but on the left, my face is about 1.5 squares wide while my face in the right image is 3 squares wide!
Algebraically, this is like we’re doubling the x-coordinates of all the vectors in the original image to get the stretched image on the right.
This is an example of a linear transformation, and eventually we’re going to see that all the information about a linear transformation can be summarized by a matrix.
We’ll see matrices next time! If you have any questions, let me know. Now let me go see Boston! See you next week!