Arithmetic with Complex Numbers
Adding and Multiplying Complex Numbers As Arrows
Today I wanted to talk a little bit more about the complex plane.
In my last two posts, I gave some background on how complex numbers were discovered, and how the imaginary unit i can represent a 90 degree rotation.
Here, I want to give some more insight on how complex numbers can represent rotations of any degree, which will lead us closer to proving Euler’s famous formula,
But first, we need to get a little more familiarity with complex numbers.
Adding Complex Numbers
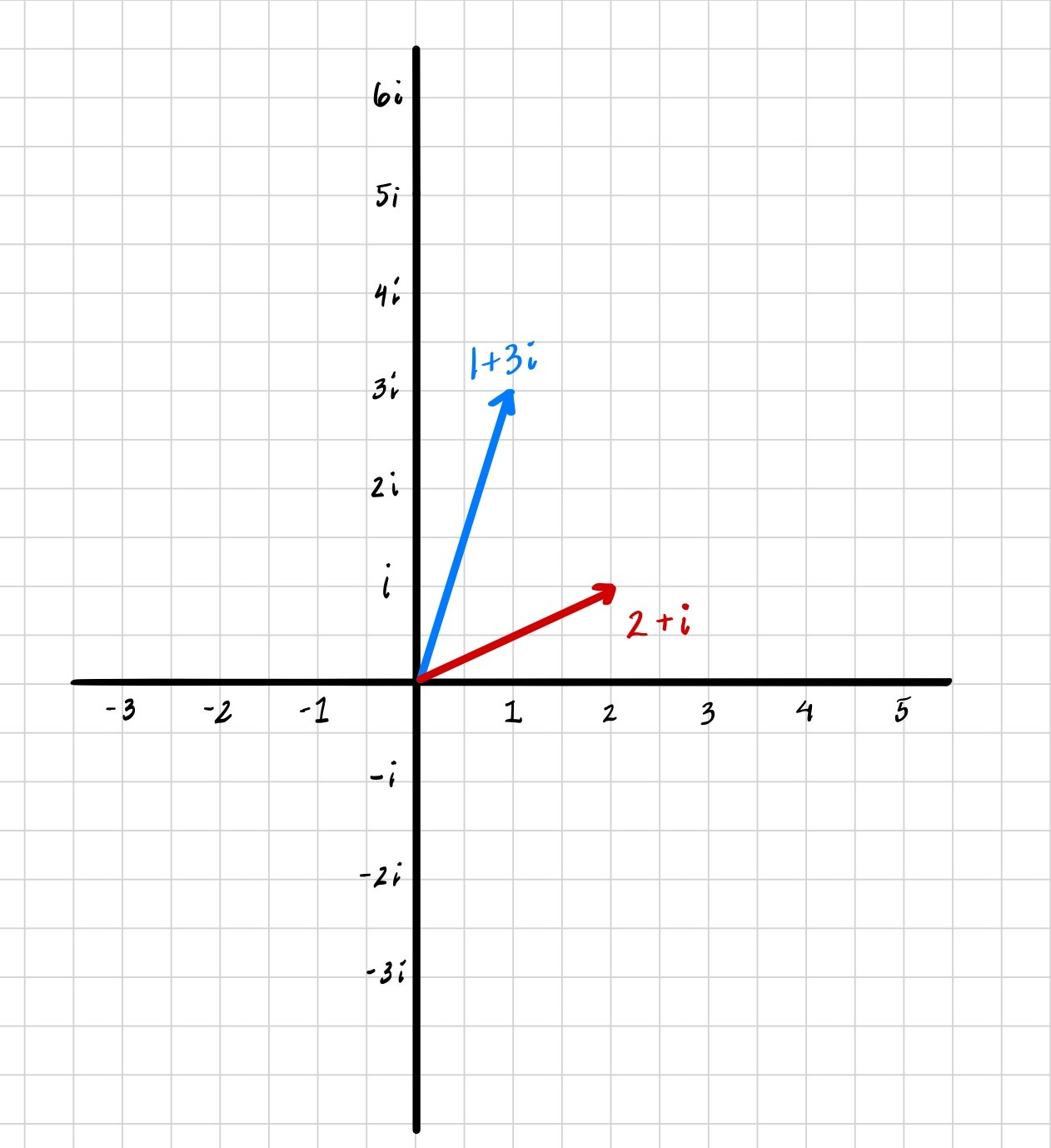
Picture each number as its own arrow starting from the origin. You can add two numbers by just stacking their arrows on top of each other, so an arrow with length 2 plus an arrow with length 4 makes an arrow of length 6.
With complex numbers, this analogy still works! When you stack the arrows together, the sum is just the third side of the triangle.
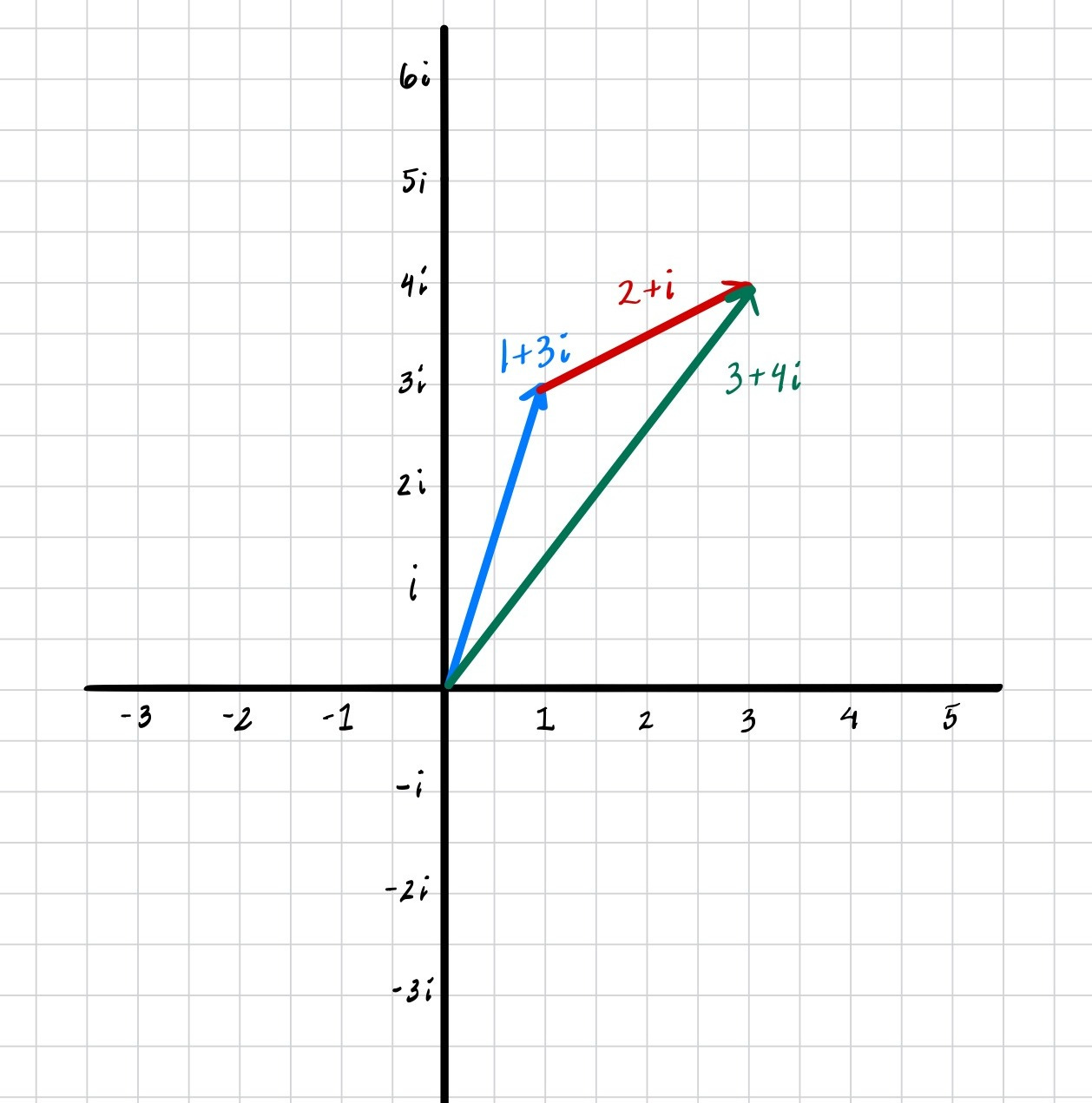
Take the complex number (1+3i) and add (2+i). Adding together their real parts (1+2=3) and imaginary parts (3i+i=4i), we get 3+4i as our answer. You can see this geometrically too:
Multiplying Complex Numbers
Okay, now the real fun happens when we multiply complex numbers, because multiplication makes the angles add up!
Let’s multiply (1+3i)(2+i) algebraically first, remembering that i^2 = -1.
What does this look like geometrically?
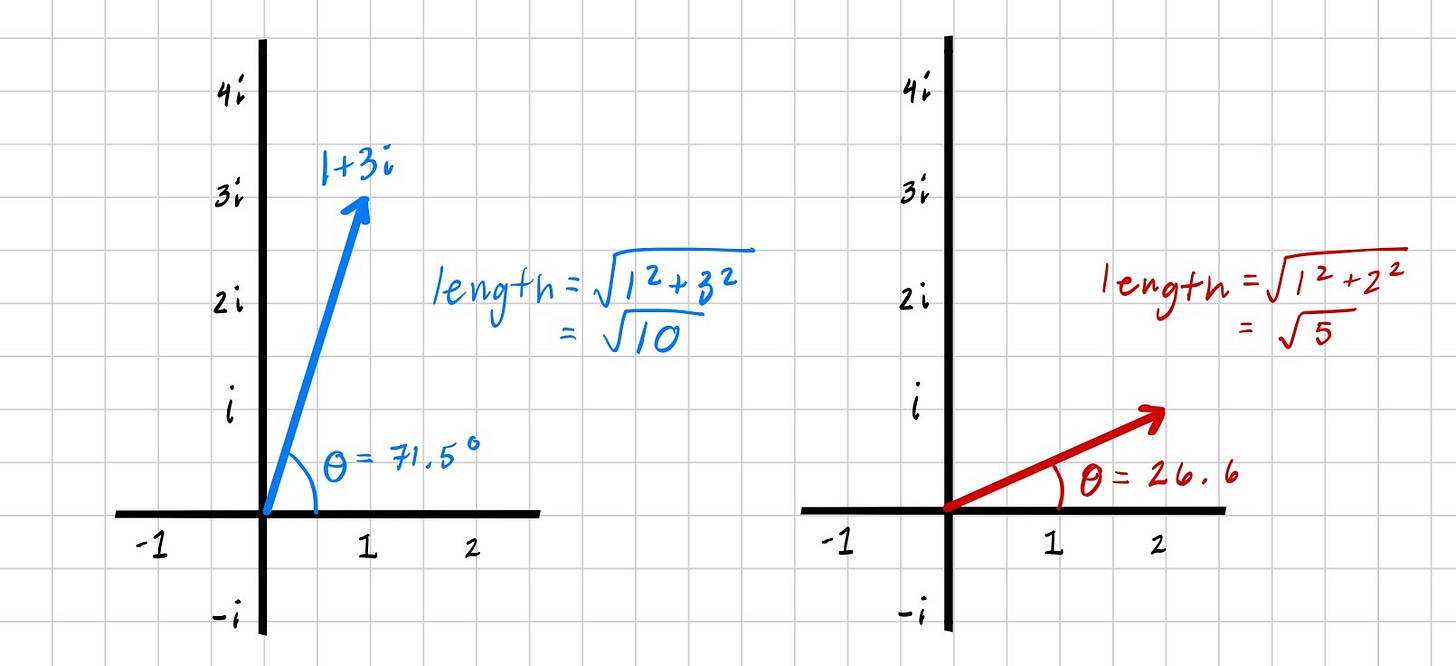
First, let’s calculate the angles of each complex number (1+3i) and (2+i). That can be easily done using the inverse tangent function. We can also calculate the lengths of each arrow by using the Pythagorean theorem:
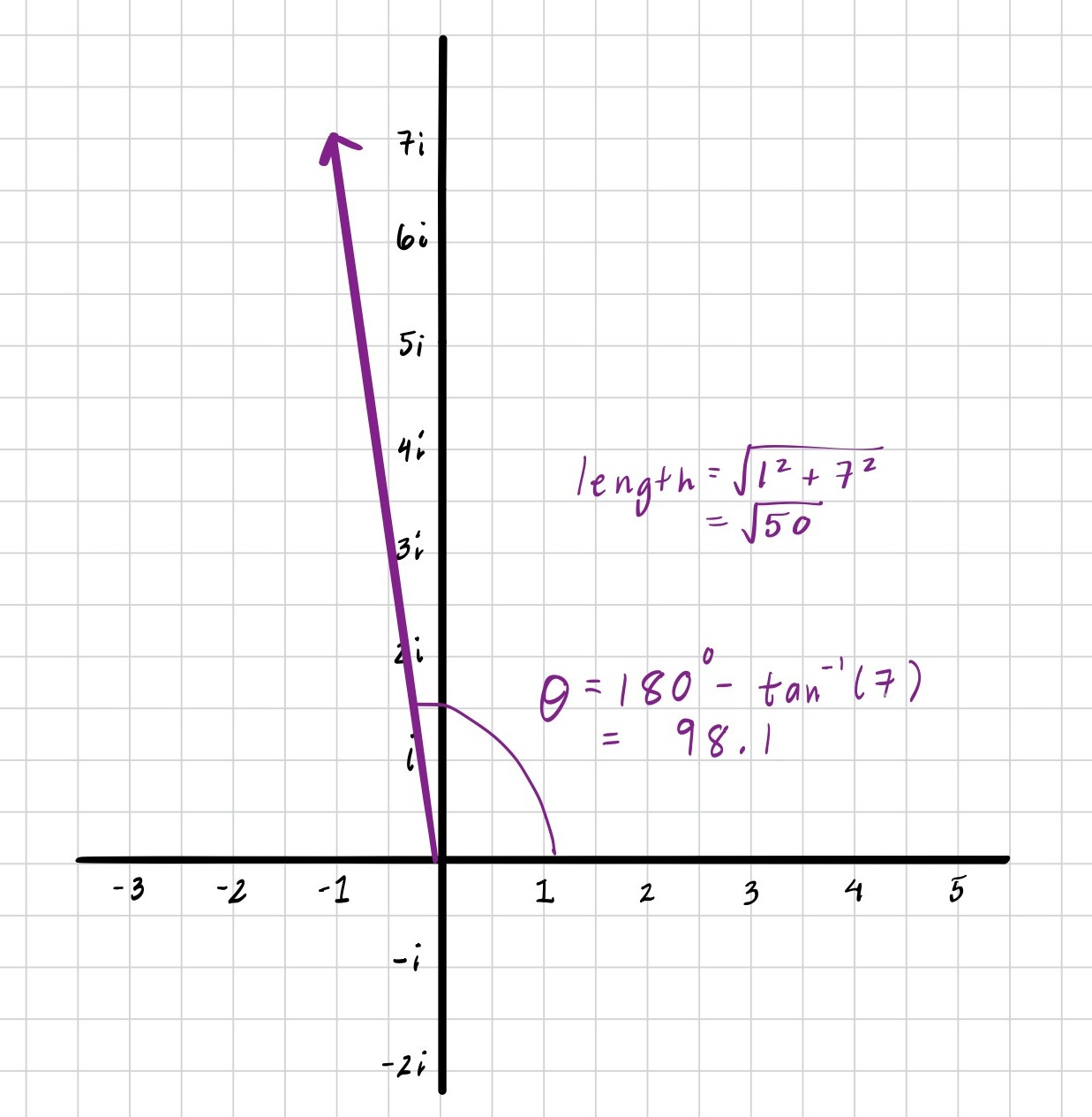
Now we can see that their product (-1+7i) is precisely the sum of the angles (71.5 + 26.6 = 98.1) and the product of their lengths (sqrt(10) * sqrt(5) = sqrt(50)):
That’s incredible, isn’t it!
In a way, it almost feels more natural to refer to complex numbers using their length and angle of rotation. This is the main idea behind this famous equation:
Many describe it as their favourite equation — it combines all the famous celebrity numbers in math. It actually is a special case of a more general equation:
For the case that θ = π
(pi represents an angle of 180 degrees, more on radians in another post!)
The right side of this equation is a way of representing a complex number with its real part (cosine) and imaginary part (sine), and the left side is a way of representing a complex number with its angle of rotation (θ). We’ll unpack this more in the future!
Until then, hope you’re all having a good week so far and I’ll see you next time!