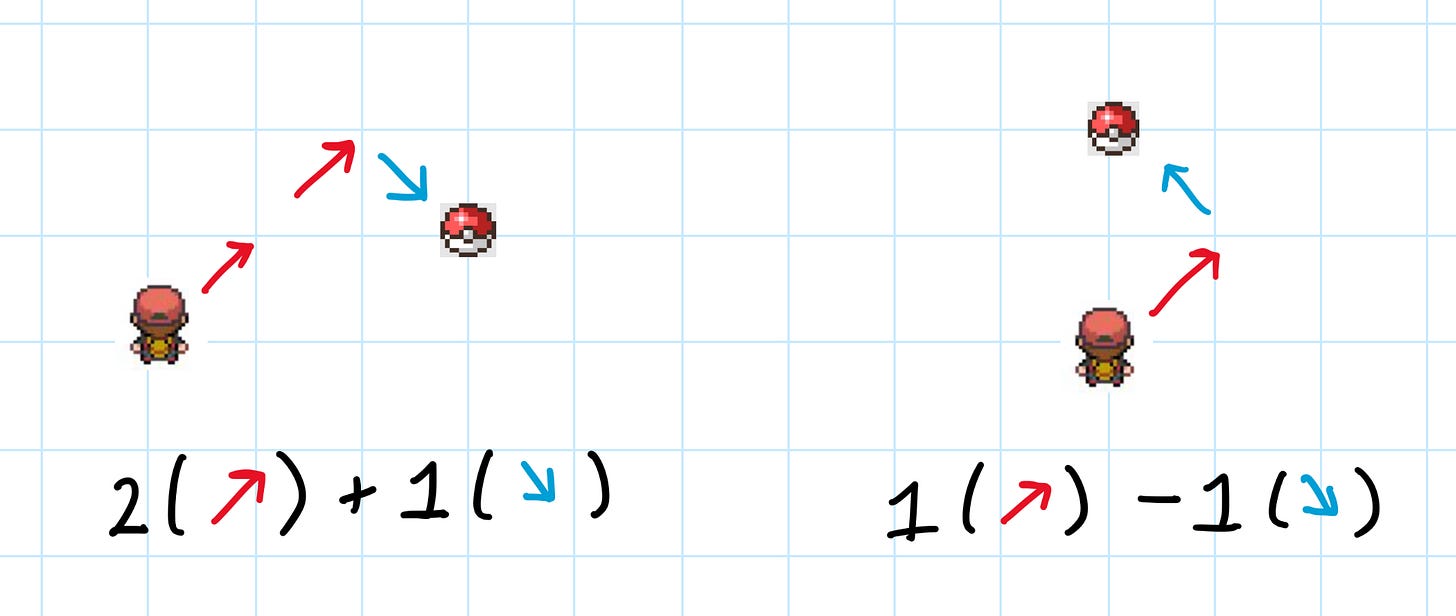My linear algebra teacher used to start off every lecture by shouting:
WHAT IS THE DEFINITION OF A BASIS?
To which we would all shout back,
A LINEARLY INDEPENDENT SPANNING SET!
And I’ve never forgotten the definition ever since.
Our goal in this post is to break down exactly what each one of those words means, with Pokemon!
I always find myself replaying my old Pokemon games. The flat, 2-dimensional world has provided me endless hours of enjoyment, despite being only able to move along two axes (left-right and forward-back).
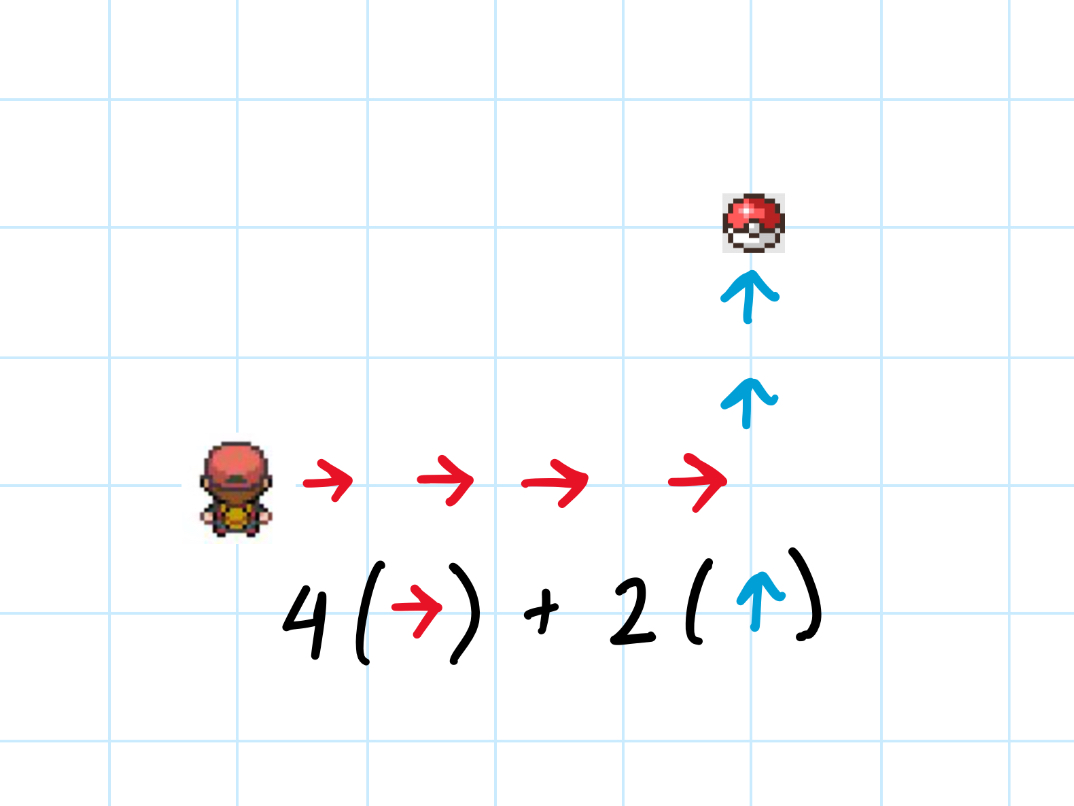
If there’s an item you want that’s 4 steps to the right and 2 steps forward, there’s no single button you can press to take you there. You have to press the right button 4 times and the forward button 2 times. We call that a linear combination - it’s just scalar multiplication combined with addition!
A single step to the right is like the vector R = (1, 0), and a single step forwards is like the vector F = (1,0). If we view the right button and forward button as vectors, then we can apply scalar multiplication and addition to get the vector 4R + 2F.
Sometimes, you need to go left and backwards, but this is like multiplying by the negatives of R and F. And negative numbers count as scalar multiples too!
We can say these vectors span this vector space. That means that every point is reachable by some linear combination of R and F.
In the game Pokemon Ranger, Nintendo gave us the ability to move our player around using a touch screen, giving us access to a whole new axis of movement. Suddenly, we could move diagonally!
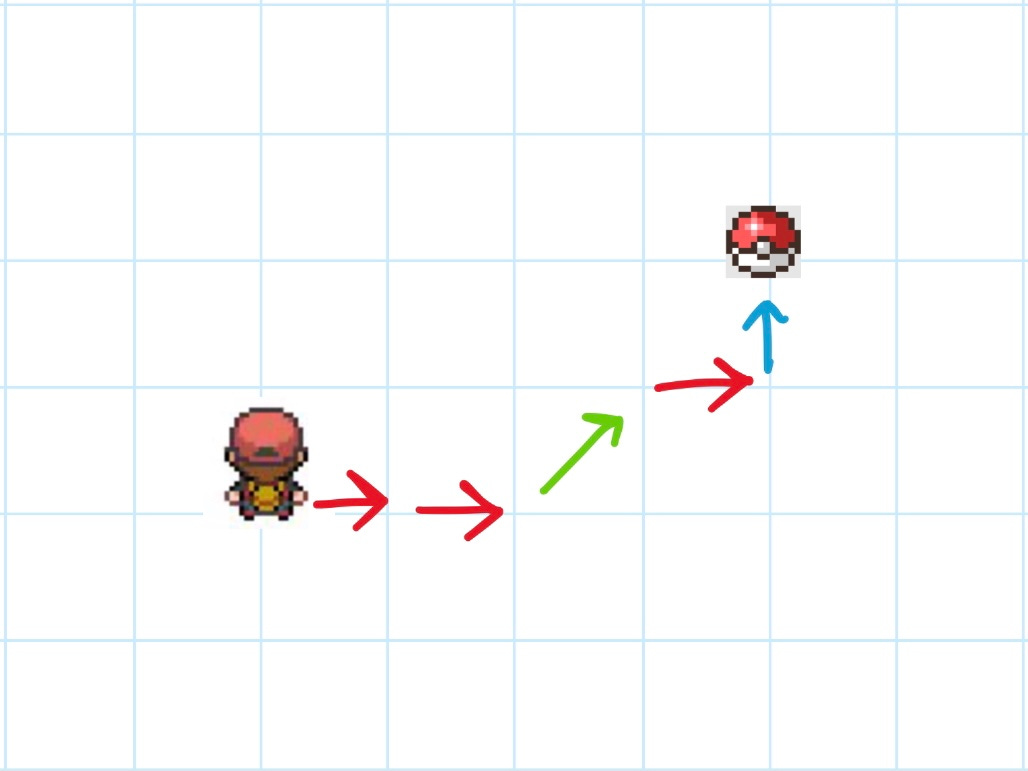
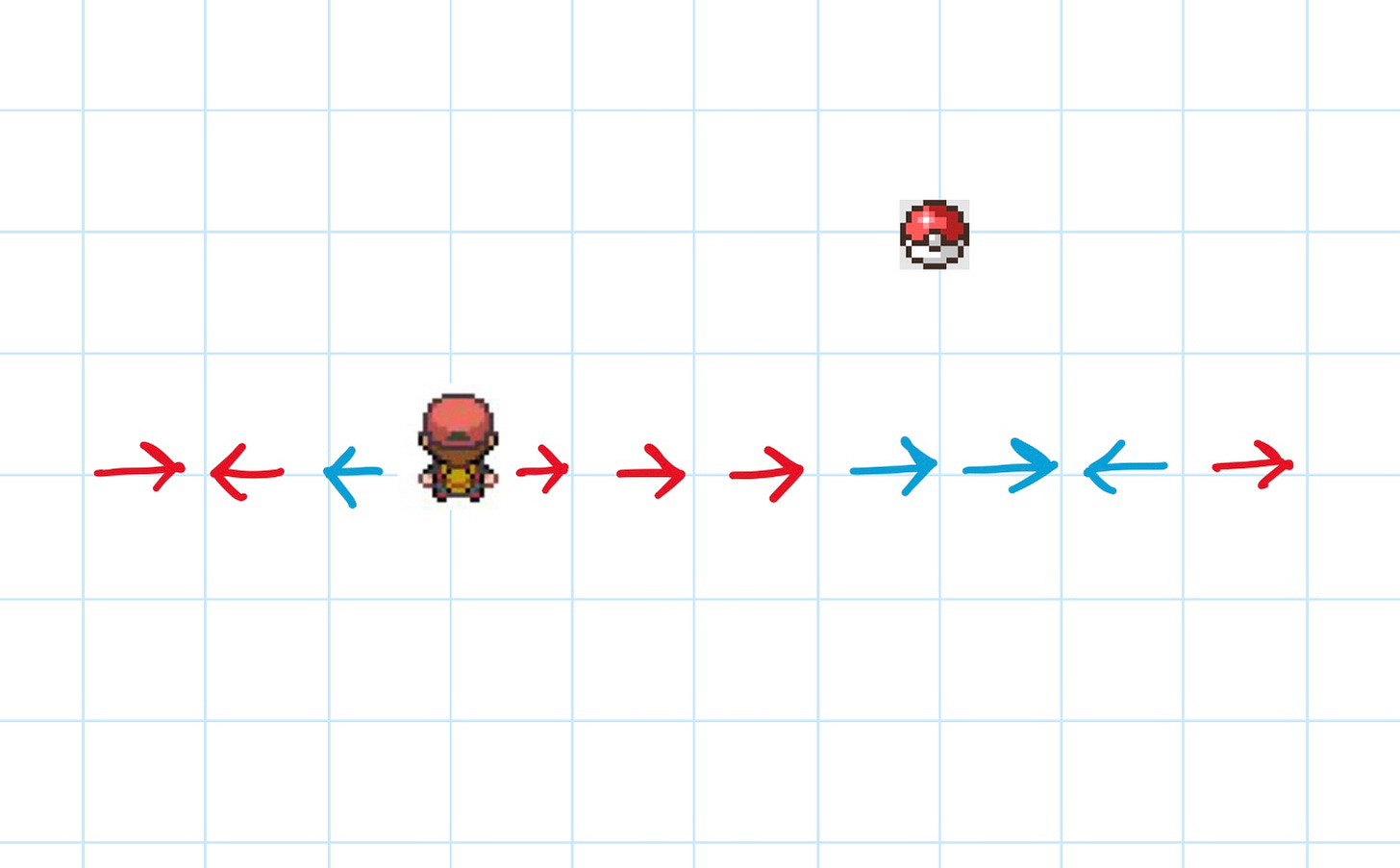
Which is a cool feature, but it’s not really necessary, is it? Any point that we can reach diagonally, we could also reach it just by travelling horizontally and vertically.
In the picture above, you can reach the pokeball just using red horizontal arrows and blue vertical arrows. The green diagonal arrow is nice to have, but it’s superfluous!
These three vectors {right, forwards, diagonal} still span the same vector space, but since the green diagonal vector is superfluous, we call it linearly dependent. That means that the green diagonal vector can be replaced by some linear combination of the red horizontal vector and the blue vertical vector.
A basis is a set of vectors that spans a vector space while also being linearly independent.
In a 2D world, your basis only needs to have 2 vectors. And they don’t even need to be the horizontal and vertical one! For instance, we could remove the blue vertical vector and still be able to traverse our world if the only directions were diagonal (along the Northeast axis) and horizontal.
If we could only move diagonally Northeast and Northwest, it would work just as well!
(Keep in mind that Northwest and Southeast are the same direction, since one is a negative of the other)
On the other hand, if our two basis vectors happened to point in the same direction, we would NOT be able to travel through the world. That’s like only being able to move horizontally.
Since the red and blue arrow fall on the same axis, they are not linearly independent, and the set containing just the two of them is not enough to span the 2D vector space!
If Pokemon was in 3D, and we could get stuff in mid air, we would need an extra set of buttons to take us up and down. To access 3 dimensions, we need to be able to move in 3 linearly independent directions.
In other words, the number of dimensions a vector space has, is the same as the number of basis vectors that’s necessary to be able to access the entire space. And this is actually how we can define the dimension of a vector space!
In the next post, we’ll look at matrices, which are the main star of linear algebra, and we can view matrices as linear transformations of basis vectors.
This post is part 3 in my series on linear algebra! Check out the previous parts: