How AI Chooses What You Watch
On machine learning, gradient descent, and collaborative filtering
When you’re swiping in or out of a video on social media, you’re engaging with an AI algorithm called a recommender system which decides what video to show you next.
How does this algorithm work?
Imagine that TikTok only had these 5 videos on the entire platform:
Imagine also that there are 5 users who are scrolling through and watching videos at their own leisure.
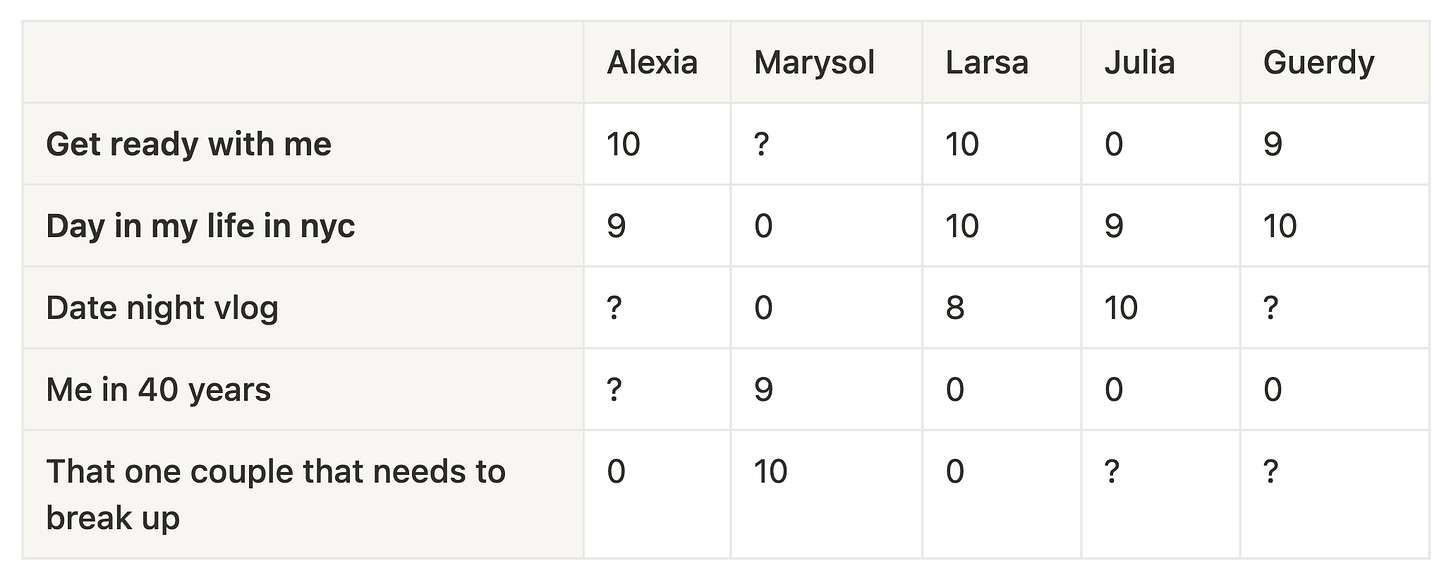
In this matrix, we’ll collect a score of how each user personally rated each video, which we might infer from their watch time, and whether they liked, commented, or shared it. A question mark is used when the user hasn’t watched that video yet.
The goal of our recommendation algorithm will be to predict what rating Alexia would give to the date night vlog and me in 40 years, so that we can show her the video she’s more likely to enjoy.
Judging by the data, it looks like she prefers lifestyle/vlog videos over comedic skits, so maybe the date night vlog would be the better recommendation.
But how to translate this into numbers?
Step 1: Quantify preferences as numbers
Let’s represent Alexia’s preferences with a vector: [x1, x2], where
x1 measures how much she enjoys lifestyle videos
x2 measures how much she enjoys comedy videos.
Suppose Alexia’s vector is thus x = [1, 0], since she highly prefers lifestyle videos over comedy videos.
Now we want to represent each video as its own vector as well:
Date night vlog = [10, 3] (10 meaning very lifestyle, and 3 meaning partially comedy)
Me in 40 years = [2, 9] (2 meaning partially lifestyle, and 9 meaning very comedy)
Step 2: Calculate predictions
Since we want to find videos that align with Alexia’s preferences, the dot product might be a suitable choice. Geometrically, it measures how much two vectors are pointing in the same direction. So lets calculate our “predictions” by taking the dot products of the vectors:
Predictions:
[1,0] * [10,3] = 10 + 0 = 10 (Alexia will rate the date night vlog a 10)
[1,0] * [2,9] = 2 + 0 = 2 (Alexia will rate the me in 40 years video as a 2)
So our recommendation algorithm all boils down to a bunch of matrix and vector multiplication, and in practice this would happen on a huge scale with matrices of thousands of rows. It’s all linear algebra!
But wait - where did all these numbers come from?
How did I choose the weights that represented lifestyle-ness and comedy-ness?
This is the part of the algorithm that can be called AI: we let the algorithm specify the weights on its own! This is done through an algorithm called gradient descent.
Step 3: Tweak the weights and parameters with gradient descent
Start by defining a loss function J(w) which measures the difference between our predicted rating and the actual ratings, and w is the vector representing the date night vlog: w = [10,3]
Suppose that when Alexia was actually shown the date night vlog, she ended up rating it a 7 instead of 10, as we predicted.
Then the loss function would be the difference between those ratings: 10-7 = 3.
Now, lets try to improve the prediction by tweaking the weights:
Let’s try replacing w = [10, 3] with [10.1, 3.1]
Let’s calculate the new prediction and thus the new loss:
[1,0] * [10.1,3.1] = 10.1 + 0 = 10.1
New loss = 10.1 - 7 = 3.1 → This prediction is worse!
Let’s tweak the weights in the other direction now, replacing w = [10,3] with [9.9, 2.9]
The new prediction = [1,0] * [9.9, 2.9] = 9.9 + 0 = 9.9
The new loss = 9.9 - 7 = 2.9 → This prediction is better!
The idea is thus to tweak the weights by little steps in whichever direction minimizes the loss function, which makes the prediction more accurate.
We can automatically pick the direction to tweak by using the derivative J’(w) (AKA the gradient), at each step replacing w with w - 0.1*J’(w)
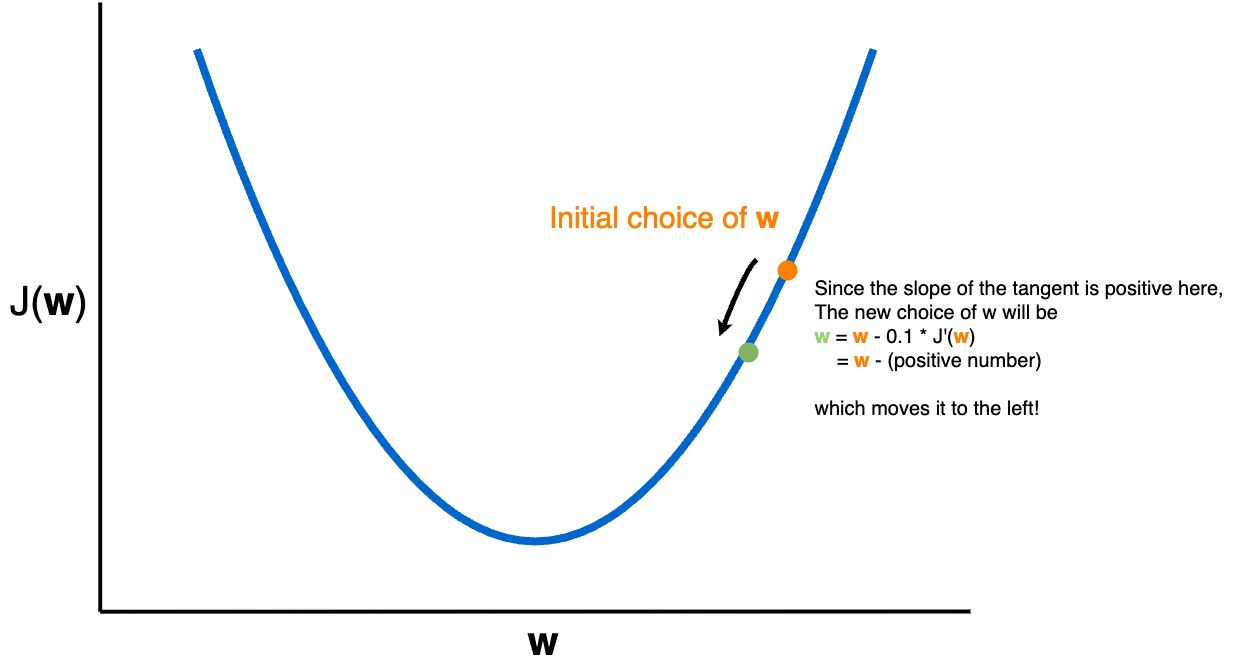
This process repeats a bunch of times, each time altering the weights by tiny steps until we reach the minimum, at which point the process would terminate because J’(w) would be zero and there would no longer be any updates to w.
One might say the algorithm is “learning” about the correct weights and numbers because the weights are not selected manually by a programmer but by the program itself. But now you know that there’s no sorcery going on here, but merely a bunch of mathematical calculations, for loops, and if-statements.
Reflections
What’s fascinating is that you can start this algorithm by choosing random numbers for w and gradient descent will automatically tweak it to match the nearest local minima.
Nobody actually has to manually decide how to categorize a video as being 70% lifestyle or 20% comedy — the algorithm learns those weights all by itself!
Also, nobody has to identify what genres are in each video either - we can automatically group videos into different genres by simply looking at what similar users are rating different videos.
This is called collaborative filtering, and is basically what happens when Netflix says, others users who liked Movie X also watched Movie Y.
The ~algorithm~ can discover new genres and categories that humans may not have even considered. Maybe a person’s preferences are more complex than just lifestyle versus comedy, maybe some users have a preference for watching videos made by creators of the same nationality as them, or maybe some users have a preference for videos of talking heads over those that are solely text on the screen.
Recent advancements made in GPU technology made it faster for computers to run lots of parallel math calculations simultaneously, which we used to think was just useful for graphics in video games, but turned out to be immensely useful for machine learning algorithms like the ones described, which involves matrix multiplications with potentially millions of users and millions of videos. By using huge datasets and a huge number of repetitions, researchers are making algorithms which are eerily accurate at making recommendations, which is hugely profitable. Google makes billions of dollars in ad revenue which is all passed through recommendation algorithms that decide which ads to show you to yield the highest profit. It’s remarkable and scary at the same time.
Funny how each of us exists online as a huge list of numbers that nobody on Earth quite understands and yet captures intimate details about who we are and what we believe, which makes it a massive violation of our privacy, a goldmine of valuable scientific and business insights, and a national security threat.