How The Complex Plane Works
Rotation and Imaginary Numbers
Today, I want to give some motivation behind how the complex plane works.
First, let’s start with thinking about a number line which extends infinitely far from negative infinity to positive infinity. It includes all the whole numbers, and all the numbers in between them.
(Because my screen isn’t infinitely large I could only fit numbers from -6 to 6, but imagine it extends infinitely far).
We can think about representing each number with an arrow that has its base at 0, and points to positive numbers on the right and negative numbers on the left.
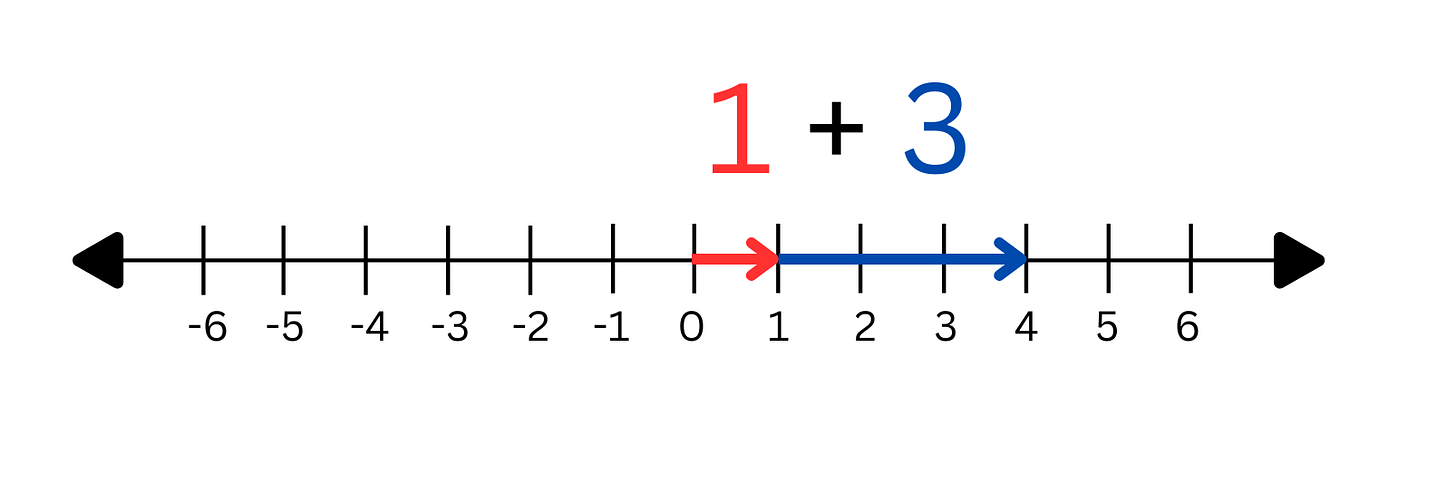
Adding two numbers together is the same thing as stacking their arrows together:
And multiplying a number is akin to scaling its arrow:
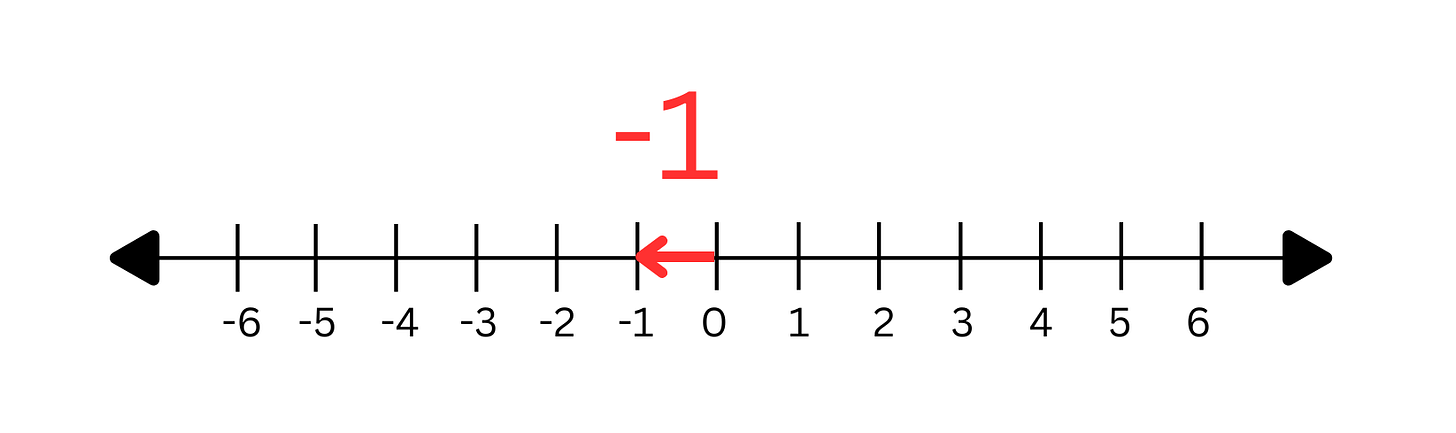
When you multiply by a negative number, it’s like flipping an arrows direction, or a 180 degree turn. Positives turn into negatives, and negatives turn into positives.
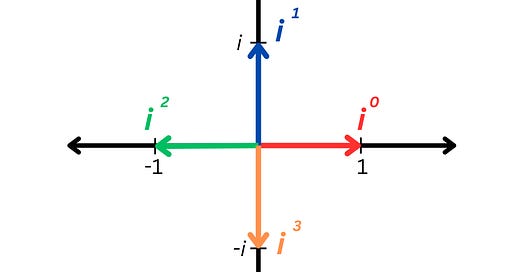
What happens when you multiply by i?
Let’s start with 1 times i, which is simply i.
Now let’s multiply by i again, and we get:
Remember, this is the definition of i.
What if we multiply by i a third time?
Finally, let’s multiply by i a fourth time:
So multiplying by i four times just brings us back to 1, where we started! It’s like doing a 360 degree turn!
If we wanted to keep multiplying by i and find the fifth power, sixth power, and so on, we would find that it would just keep cycling through these four numbers:
We can visualize all of this by thinking of i as a 90 degree rotation:
So we’ve seen that i does not live on the number line — it lives on a whole new axis!
The new vertical axis we’ve introduced is called the imaginary numbers, and the horizontal number line is called the real numbers.
All the space in between? Those are the complex numbers! They’re made of a real number plus an imaginary number.
And that’s the complex plane! Complex numbers have their own rich internal structure, and we will see that there are complex numbers which can represent rotations of any degree!
But that’s all for today’s post!