Infinity Comes In Different Sizes
Why Some Infinities Are Bigger Than Others, Explained With Wigs
There are infinite numbers between 0 and 1. There's .1 and .12 and .112 and an infinite collection of others. Of course, there is a bigger infinite set of numbers between 0 and 2, or between 0 and a million. Some infinities are bigger than other infinities.
- John Green, The Fault in Our Stars
There are infinitely many examples of infinite sets. Here’s a few:
The set of natural numbers: 1, 2, 3, 4, 5, 6, and so on
The set of even natural numbers: 2, 4, 6, 8, 10, 12, and so on
The set of numbers between 0 and 1
The set of numbers between 0 and 2
Are some infinite sets larger than others? Was Hazel Grace Lancaster onto something here? It depends on how you count infinity.
The 19th century Russian mathematician Georg Cantor proposed a method of answering this question by using one-to-one pairings, called bijections.
Example: Counting Wigs
Suppose I hand you a box of wigs and a box of mannequin heads, and your job is to find out whether there’s an equal number of both. You could start by counting each wig and mannequin head one by one, but let’s pretend for now that you’ve lost your ability to count past the number 3. Is it still possible to still determine whether there’s an equal number of wigs and heads?
Yes, just pair them up by putting a wig on each head! Then you will be left with 3 possibilities:
You run out of heads, and there are wigs leftover. Then # of wigs > # of heads
You run out of wigs, and there are bald heads leftover. Then # of wigs < # of heads
You put a wig on each head and each head has a wig. Then # of wigs = # of heads
Using one-to-one pairings, we can compare the sizes of infinite sets without needing the ability to explicitly count them. This brings us to the concept of countable infinity, the smallest infinite set.
Countable Infinity
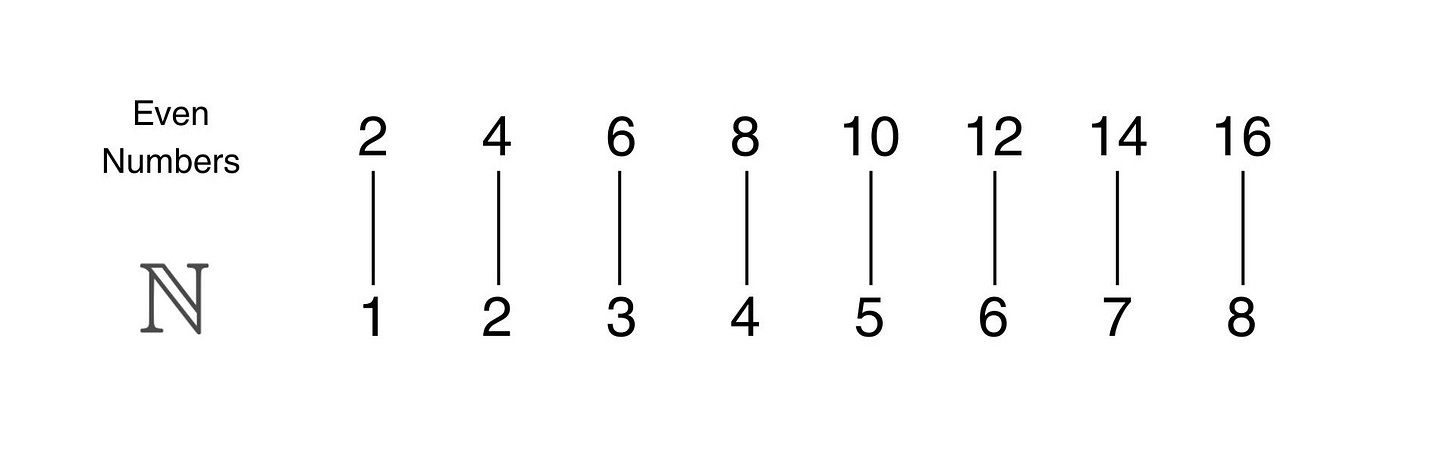
A set is said to be countably infinite if you can pair up its elements with the set of natural numbers: {1, 2, 3, 4, 5, …}. This set is denoted by a fancy capital N.
The set of even numbers is countably infinite, despite the fact that they are a proper subset of the natural numbers, because you can pair them up like this:
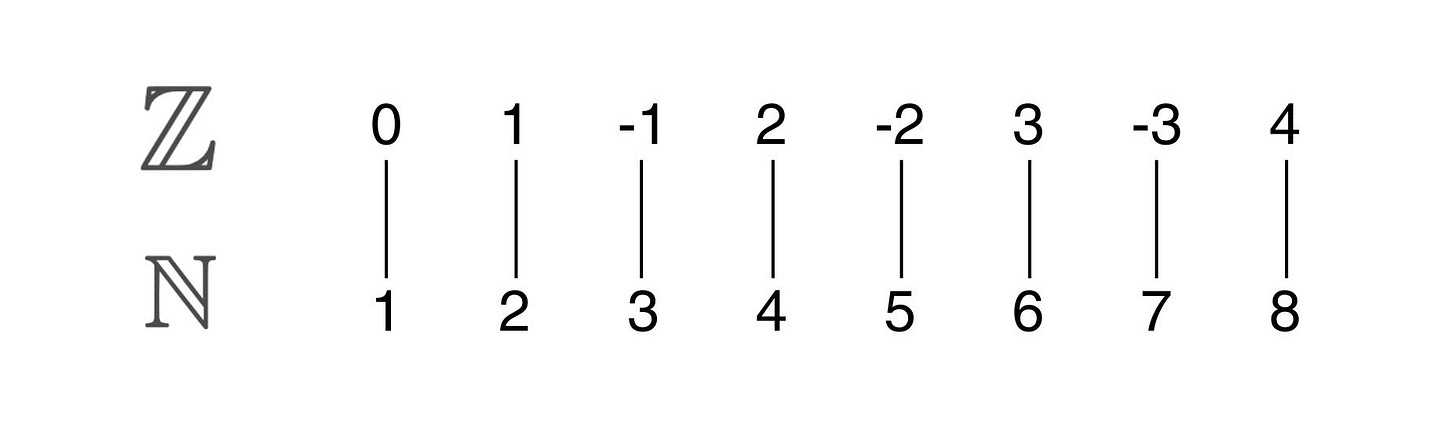
So is the set of integers (Z), which we can pair with natural numbers by starting at 0 and then hopping back and forth between the positive and negative side.
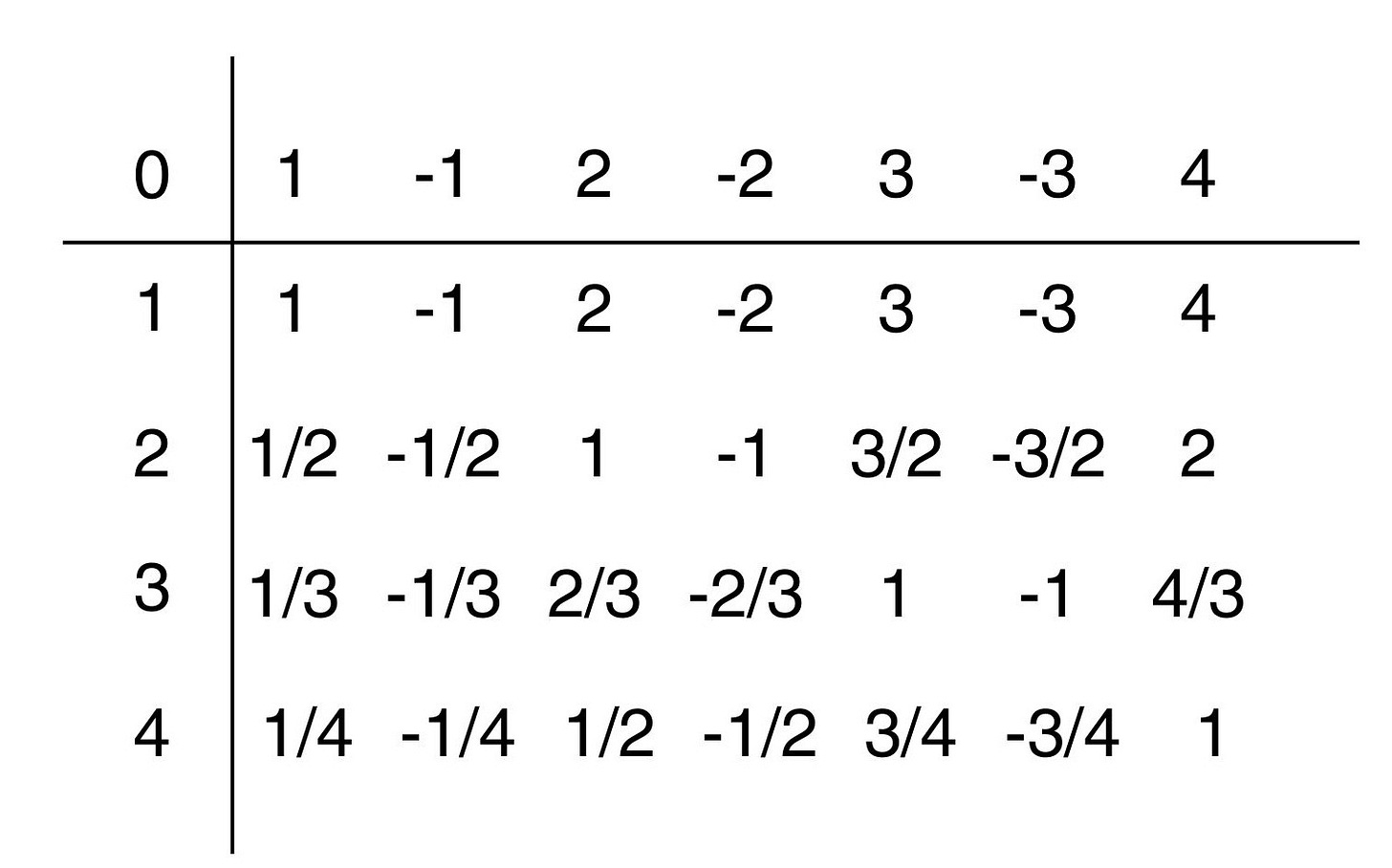
Surprisingly, the set of rational numbers (denoted by the fancy Q) is countable too. Unlike the whole numbers which stand separately like islands, the rational numbers are packed densely. There’s no next rational number after 0, because there’s 0.1, or 0.01, or 0.001, and there are infinitely many more rationals to choose in between. However, it is possible to pair them up with the natural numbers by first remembering that each rational number can be expressed as a fraction p/q, where p is an integer and q is a natural number. We can put them all on a grid with the possible numerators p on the horizontal axis and all the possible denominators q on the vertical axis, with all entries of the grid being all the possible fractions p/q.
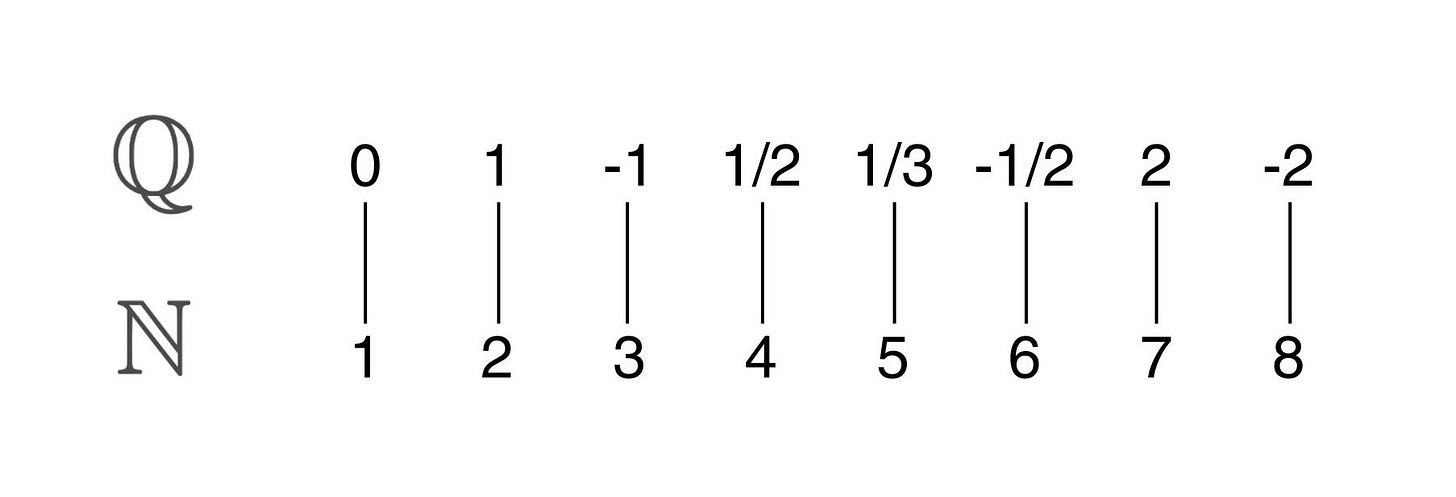
Then pairing the rationals with naturals is easy, because you can just wind your way through the grid like a snake, skipping over any fractions that have already been counted.
Then the enumeration looks like this:
A set which is countably infinite can be said to have a cardinality of aleph-0. That’s the size of the set of natural numbers, also the size of the smallest infinity.
Uncountable Infinity
If a set is neither finite nor countably infinite, then it is uncountable. The set of numbers between 0 and 1 is the classic example of an uncountably infinite set. It is a continuum of numbers which really has no next element, no matter how cleverly you try to order them.
That’s because of all the irrational numbers in it. Unlike rationals, which can be expressed either as a fraction or as a decimal number which repeats (⅓ = 0.333…) or terminates (½ = 0.5), irrational numbers are those numbers like pi, which have infinitely many digits that cease to repeat.
The set of real numbers is the whole number line which includes both rationals and irrationals.
If you tried to pair these up with the natural numbers, you would run out of numbers. There would be real numbers leftover, just like wigs left without a head to sit on! The proof of this is famous. I’ll give a brief sketch of it here.
Cantor’s Diagonalization Argument
We’ll start the proof by first assuming that the set [0,1] is indeed countable, and then showing that this countability falls apart.
Step 1: Assume that the set [0,1] is countable. If so, then there must be a way to pair up the set with natural numbers, such as the following
Step 2: Show that this assumption falls apart, by finding a number in [0,1] which is not on the list.
Let’s call this new number k. We will build k by forcing it to disagree with each number on the list, so that the nth digit of k is always different from the nth digit of the nth number on the list. Here’s an example:
If you look at the diagonal entries on the list to the right, the numbers are 1, 3, 9, 3, 3, 4, 1, 0, and so on. We build k by explicitly avoiding the same digits, so we use a 7 whenever there’s a 3, and a 3 whenever there’s a 7 (or any other digit). You could do the same thing with 0 and 1 or any other pair of digits.
This ensures that k is different from every number on the list. Therefore, k is not on the list! It is a wig without a head, and proof that the interval [0,1] is uncountable.
The Fault in The Fault in Our Stars
In the context of Cantor’s set theory, some infinities really are bigger than others, but the interval [0,1] is the same size infinity as the interval [0,2] and [0, 1000000]. They all have a cardinality of c. What Hazel could have said is that there’s the infinite number of stars in an endless sky, but then there’s the bigger infinite number of points between the stars.
More Mysteries
There are even bigger infinities than c! For instance, the number of possible subsets of real numbers is greater than the number of real numbers. You can build a ladder of greater and greater infinities.
One unanswered question is whether there is a set whose cardinality is greater than the aleph-0 but smaller than c. This is called the continuum hypothesis.
Infinity is larger than we imagine, smaller than we imagine, and queerer than we imagine! I find it infinitely fascinating.