What is the most efficient route for a drag queen touring across the country?
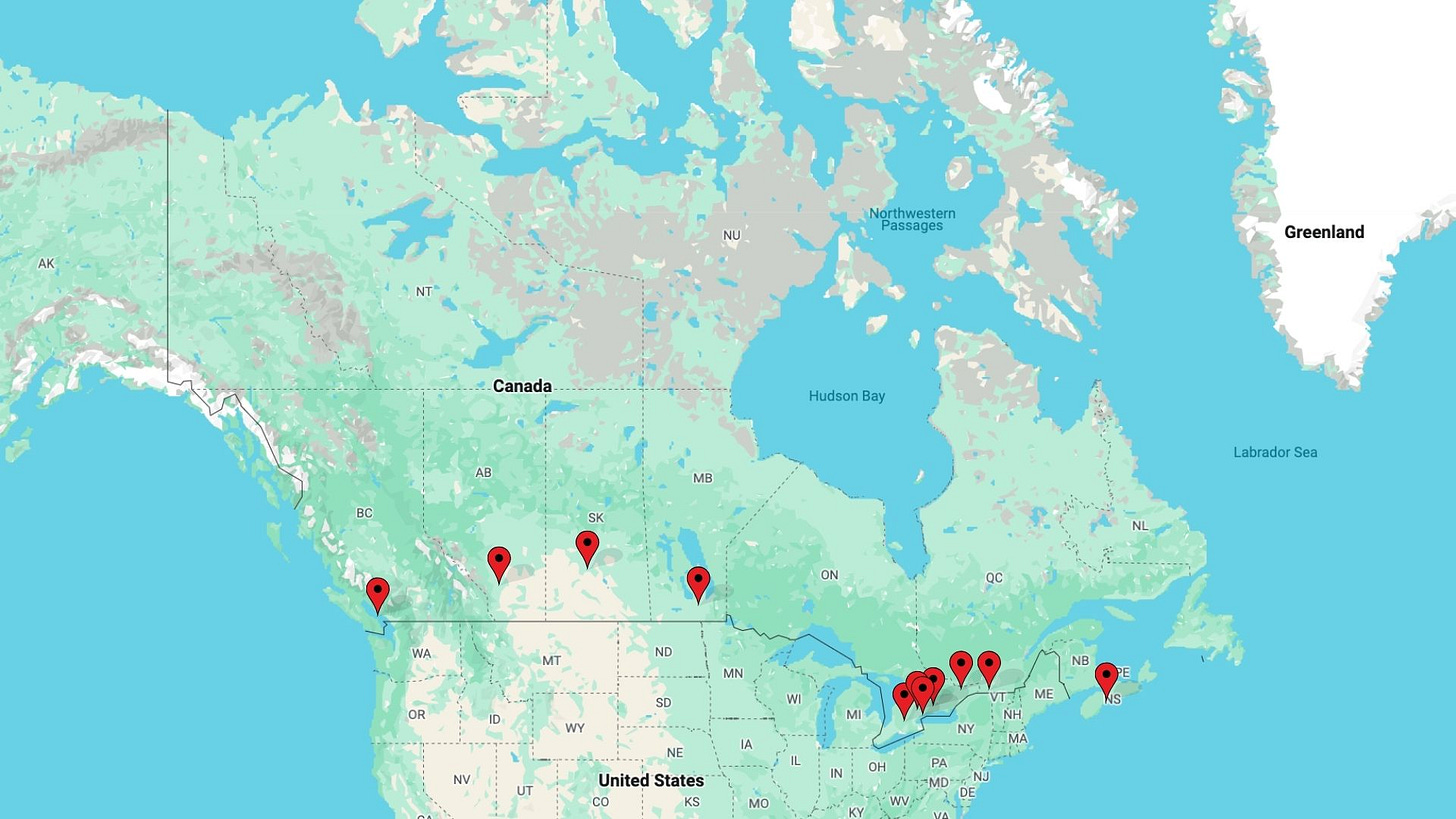
I’ve just returned home from a cross country road trip where I visited 11 independent bookstores to promote my book, Math In Drag! Me and my husband did it as a road trip cause we like the flexibility of stopping wherever we want. We got to see up close the beauty of Canada, from the Rocky Mountains in Banff National Park to the World’s Largest Coca Cola Can in Portage la Prairie, Manitoba.
An important question to consider if you’re a drag queen on a dime like me is how to best plan your route to minimize the distance and save costs.
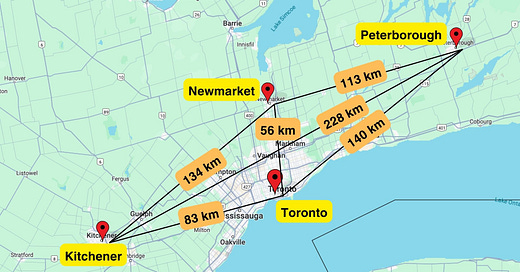
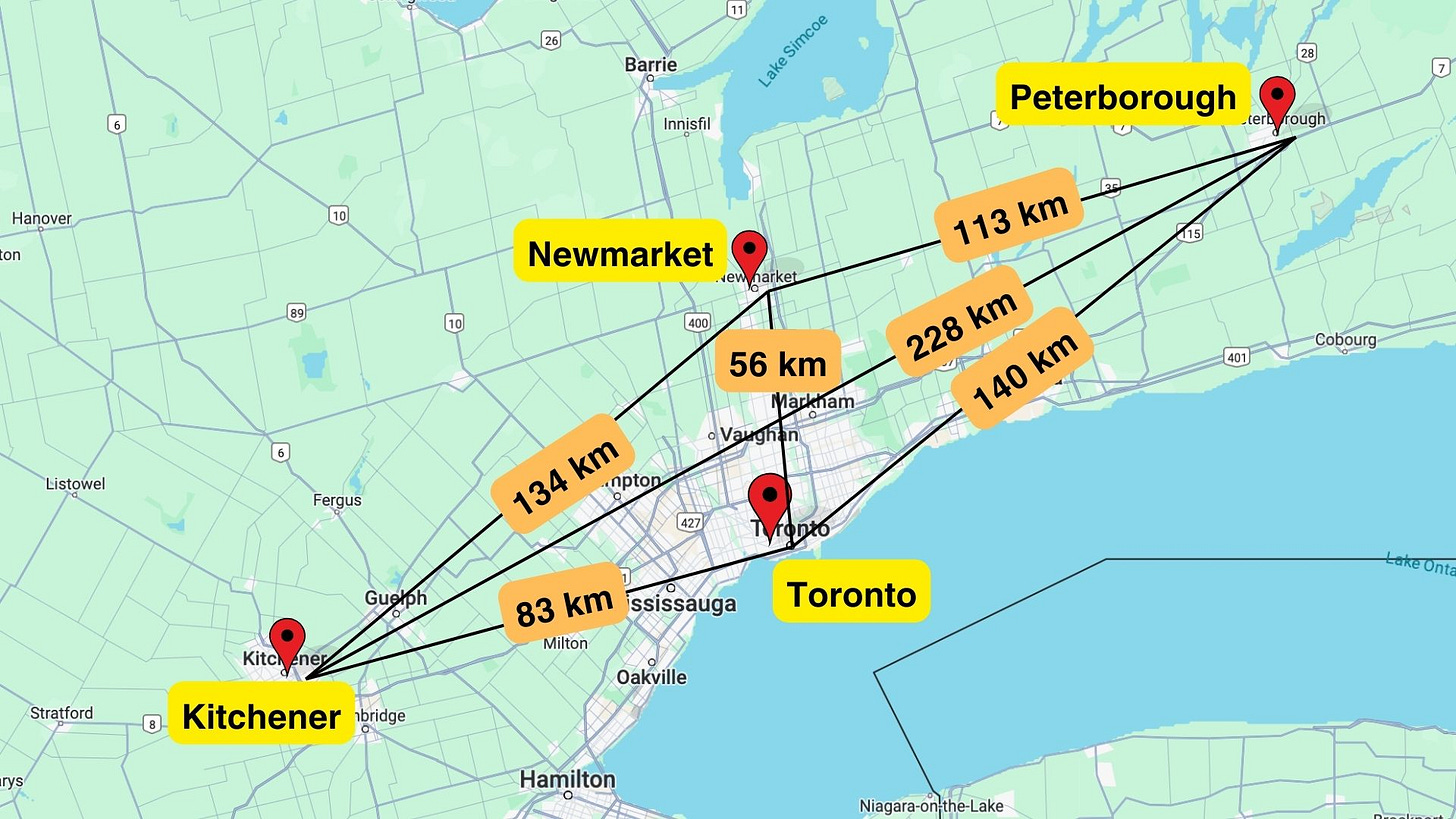
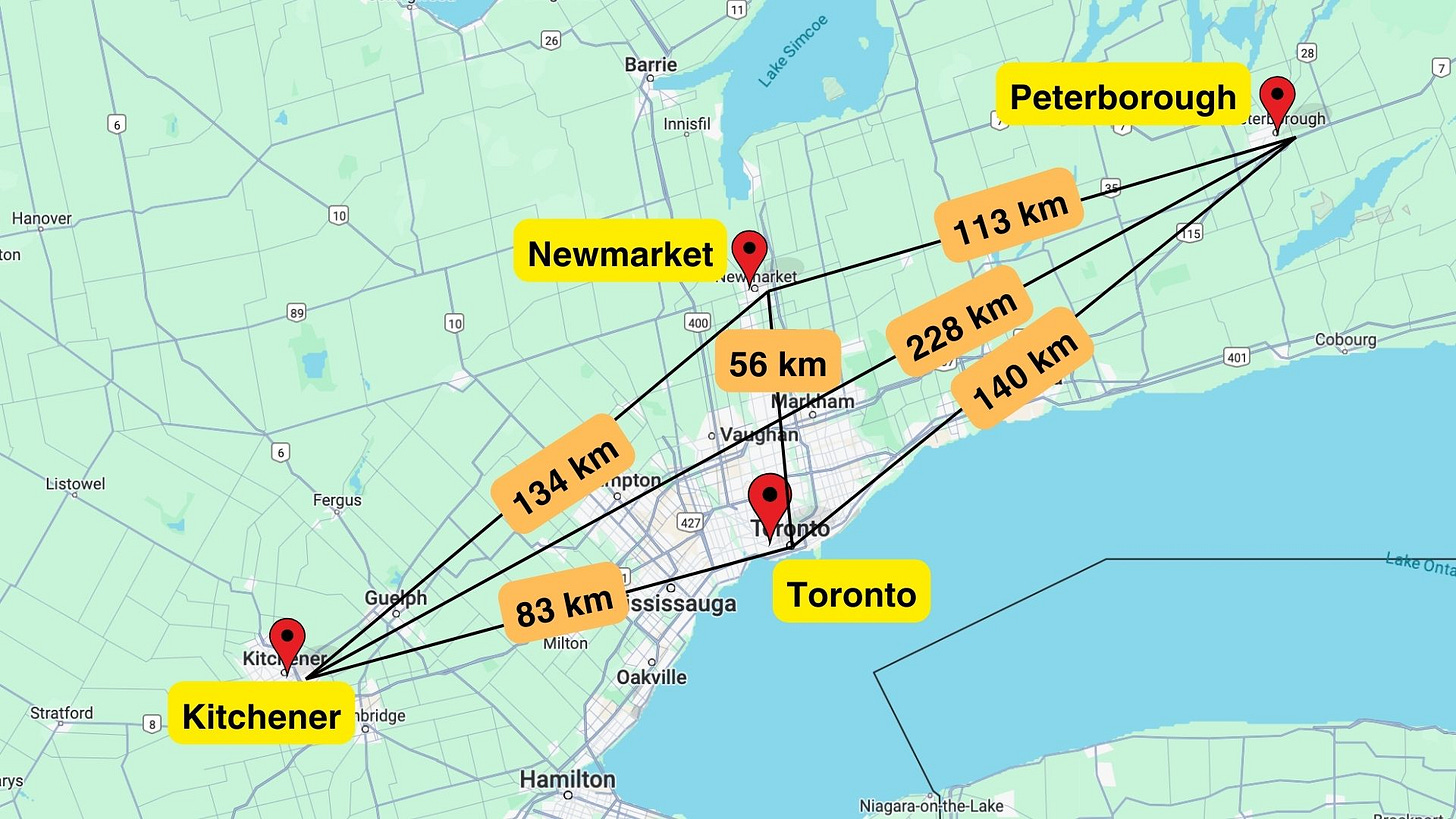
Consider the first four cities we went to: Kitchener, Toronto, Peterborough, and Newmarket. Can you find the shortest path that goes through all 4?
By inspection, the shortest path goes from Kitchener → Toronto → Newmarket → Peterborough. The length is equal to 83 km + 56 km + 113 km = 252 km.
To confirm that this is the shortest path, you can compare it to all possible paths.
The number of possible paths is 4 factorial, or simply 4!, which equals 4*3*2*1. There are 4 possible starting points, and then once you choose the starting point, you have 3 options for which city to visit next, and then 2 options for the third city, and then 1 final city to visit last.
However, the path from Kitchener → Toronto → Newmarket → Peterborough has the same distance as doing the exact reverse, from Peterborough → Newmarket → Toronto → Kitchener, so we can cut the list in half and only have to check 12 paths to confirm that this is the shortest one.
Kitchener → Toronto → Newmarket → Peterborough = 252 km
Kitchener → Toronto → Peterborough → Newmarket = 336 km
Kitchener → Newmarket → Toronto → Peterborough = 330 km
Kitchener → Newmarket → Peterborough → Toronto = 387 km
Kitchener → Peterborough → Toronto → Newmarket = 424 km
Kitchener → Peterborough → Newmarket → Toronto = 397 km
Toronto → Kitchener → Newmarket → Peterborough = 330 km
Toronto → Kitchener → Peterborough → Newmarket = 424 km
Toronto → Newmarket → Kitchener → Peterborough = 418 km
Toronto → Peterborough → Kitchener → Newmarket = 502 km
Newmarket → Toronto → Kitchener → Peterborough = 367 km
Newmarket → Kitchener → Toronto → Peterborough = 357 km
Indeed, 252 km is the shortest path. But that’s just for the first 4 cities.
What about my 11 city tour?
With 11 cities, the number of paths we’ll have to check is 11!/2, which is 19,958,400.
I won’t try to write them all down anymore! Luckily, most of Canada falls along a straight line, so it’s a bit easier to solve this one just by intuition.
What about 48 cities?
Okay I know I’m not famous enough for this big of a tour. But consider a hypothetical road trip that visited all 48 state capitals of the contiguous states in the US. Can you find the shortest path that visits all 48 stops?
It’s not so easy to solve by eye anymore. How fast can a computer do it? Well, the number of possible paths to check is 48!/2, which is an insanely large number:
6,206,957,796,268,036,335,431,144,523,686,687,519,260,743,177,338,880,000,000,000.
That’s about 6 * 10^60, or 6 novemdecillion possible paths to check.
If you had a computer that was capable of checking a trillion paths each second, it would still take 196,821,340,571,665,282,072,271,198,747,041,080,646,269 years to check all of them!
This is the nature of the Travelling Drag Queen Problem (more commonly known as the Travelling Salesman Problem). And travelling drag queens/salesmen aren’t the only application! This problem has applications to DNA sequencing, manufacturing microchips, and setting up telecommunications networks.
Solutions
Since brute force isn’t going to give us any solutions within this lifetime, it’s better to settle for the second-best solution, or at least a good enough solution.
One algorithm we might use to solve the Travelling Drag Queen Problem can be called the Nearest Neighbour Algorithm, which goes: Starting from a random starting point, visit the nearest unvisited city.
How would this algorithm work with our 4-city problem?
If you start with Kitchener, the nearest city is Toronto (83 km), and the nearest city to Toronto is Newmarket (56 km), and from there the last unvisited city would be Peterborough (113 km). That provides us with the shortest path, which is 252 km long.
But what if we used Toronto as the starting point? The nearest city to Toronto is Newmarket (56 km), then the nearest unvisited city from Newmarket is Peterborough (113 km), leaving Kitchener as the last stop (228 km). The total length of this road trip would be 397 km, which is 58% longer than the shortest possible path!
The Nearest Neighbour Algorithm works better depending on which starting point you choose, and every map is different.
Computer scientists are interested in discovering new algorithms, and finding out which algorithms work best under which circumstances.
Some scientists have even ran experiments on pigeons and ants to see how they solve the problem!
It remains one of the most widely studied math problems in computer science and optimization.
Now you know why I’m not doing a US book tour!