What is Calculus?
The Basics of Differential and Integral Calculus
Fun fact: the word “calculus” is related to the words “chalk”, “calculate”, and “calcium”.
When a math problem is too hard to do in your head, you use a calculator. But before we had calculators, we used rocks (like an abacus). So the word for using a calculator, actually means using your rocks!
The root word for calculus is calx, which is a particular kind of rock that we used to use for counting. It’s made up of the same stuff chalk is made of, and calcium.
But what is calculus? I asked ChatGPT, and it says that calculus is the study of change, which I disagree with.
I think calculus is more about the study of infinity, and infinite processes. In this post, I’m going to try and summarize what calculus is really about.
Calculus comes in 2 flavours: integral calculus and differential calculus. They evolved to answer 2 major problems:
The Area Problem: what is the area of a curved shape?
The Tangent Problem: what is the slope of the tangent at a particular point on a curve?
The big punchline of calculus is that these two problems are actually closely related—they are inverses of each other! Now let’s look at them more closely.
The Area Problem
How do you find the area of a curved shape? Maybe you think to approximate it with a rectangle, which you do know how to find the area of: it’s just length times width.
But this isn’t an exact fit. You could use more rectangles, which would make the error smaller.
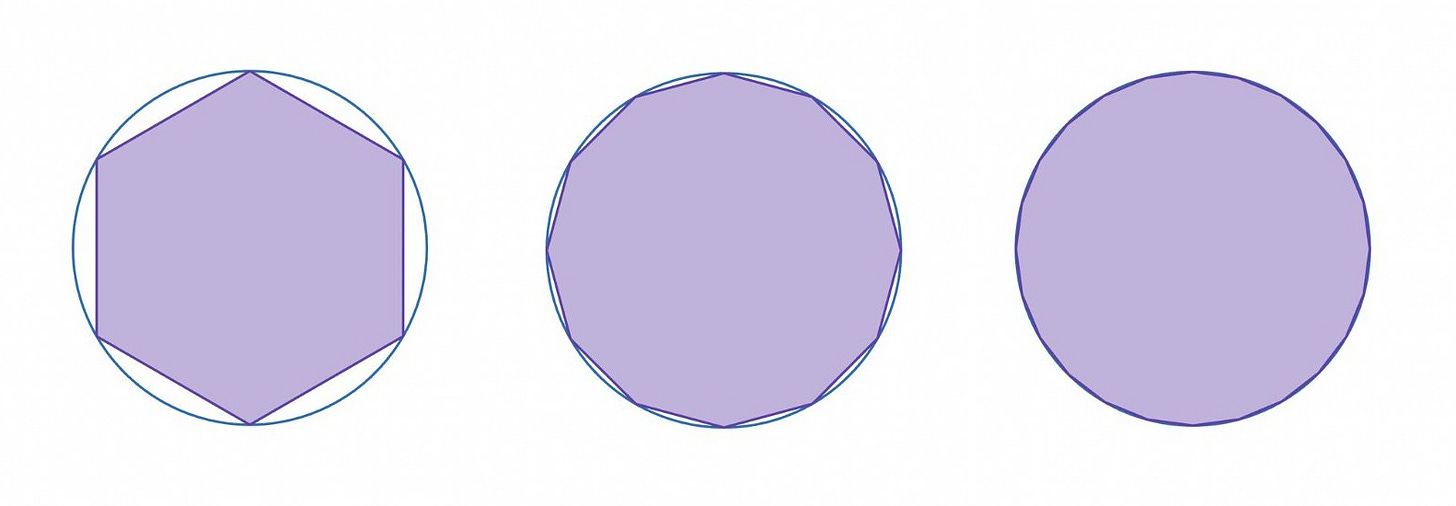
This method is how the Ancient Greeks calculated digits of π. Eudoxus and Archimedes used an infinite process, making polygons with increasingly many sides, and the desired result (the circle) was the limit of that infinite process.
To calculate the area under a curve f(x), between the interval [0,2], we use a similar method of exhaustion, by splitting it up into thin rectangular slices.
Solving the area problem boils down to adding up all the areas of these rectangles. Each rectangle’s height is just the curve f(x), and as for the width, we’ll label that Δx, which is just the size of the whole interval [0,2] divided by the number of partitions.
This formula is called a Riemann sum. But in order to get the exact area, instead of using 6 or 24 or 48 rectangles, we actually want to take the limit of this sum as the number of rectangles goes to infinity and the width Δx goes to zero. The notation for it looks like this:
This is called an indefinite integral. It’s still just a sum of areas of rectangles! The Σ sum gets replaced with a fancy new S-shape symbol to indicate that we’re now taking a sum over a continuous range of values for x. The height of each rectangle is still f(x), but the width is now dx, which represents an infinitesimal width.
The word “integral” should remind you of integrity, unity, and combining different things to become a whole. Integral calculus is about using these infinite sums not only to solve the area problem, but it can be used to solve problems about volumes, lengths of curves, population predictions, forces on a dam, and more!
The Tangent Problem
How do you find the slope of a tangent to a point on a curve?
This is the problem that has more to do with change, and is why people think calculus is all about rates of change.
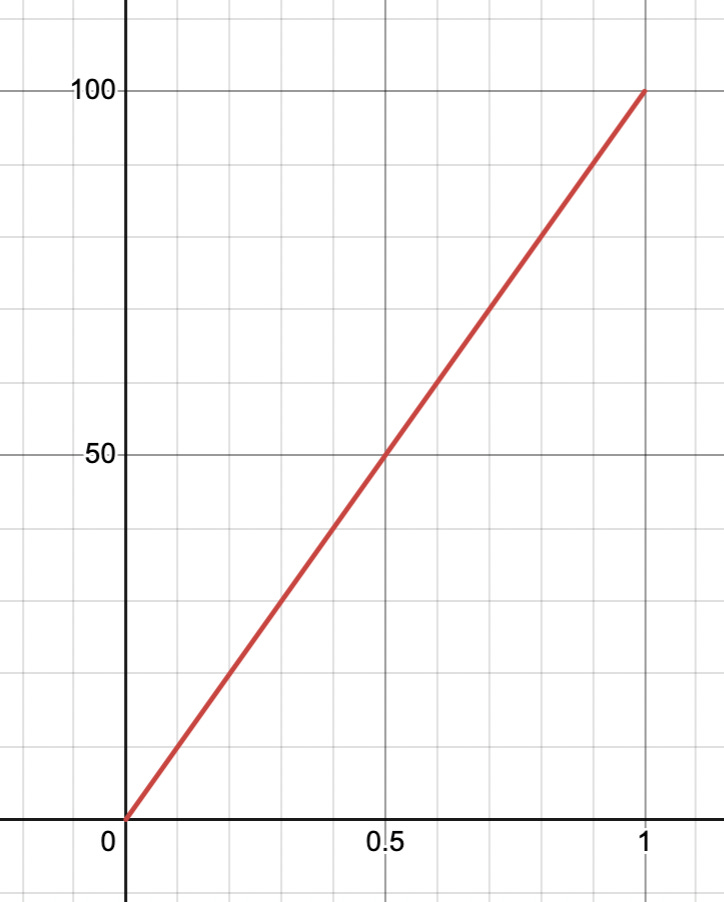
The classic example is to imagine the motion of a car. Your commute takes you 1 hour and is 100 kilometres away, so if we were to make a graph of position versus time, it would look like this:
Your speed is just the change in distance divided by the change in time, or equivalently, the change in y divided by the change in x:
The Δ symbol (delta) is often used to represent a change.
In this example, the speed is 100 km/h, which is the same as the slope of this line. In differential calculus, we refer to that as the derivative.
Now imagine an alternative scenario, where during your commute, you hit bumper to bumper traffic which slows you down for a while, and to make up for it, you speed the rest of the way to make it to work on time. Now the graph looks more like this:
Even though you still travelled a total of 100 km in an hour, your speedometer read 0 km/h while you were stuck in traffic, and it read over 120 km/h while you were speeding. That’s because your car is reading your instantaneous speed, not your average speed. That’s the same thing as your speed at a single moment in time, or the slope of the tangent to the curve.
The tangent problem is interesting because there are lots of times when we’re interested in how a quantity changes.
Examples: Is the number of daily new COVID cases rising or falling? Is the stock market trending upward or downward? Is my drag getting better or worse?!
If the answer is “rising/upward/better”, then we can assign the slope with a positive number. If the answer is “falling/downward/worse”, then assign a negative number. If the answer is “staying the same”, then assign a slope of 0.
The slope of the tangent line is called the derivative (or gradient).
As the point P traverses the curve on the left, it’s like we’re zooming into the tiny neighbourhood around P where the curve looks like a straight line (on the right), and the slope of this line is the derivative.
To calculate the derivative, or the slope in this very tiny, zoomed in neighbourhood, we’ll alter our formula to use dy and dx instead of Δy and Δx, to indicate that these are infinitesimal changes.
Differential calculus is all about solving the tangent problem, and finding these slopes, AKA derivatives. The process of converting a function into its derivative is called differentiation, and a differential is a small, infinitesimal change.
A Grand Finale
Differential calculus was invented some 2000 years after integral calculus. Humans have been trying to solve the area problem since at least the 4th century BC, whereas the tangent problem was developed in the 17th century AD.
The big reveal of calculus is that the area problem and tangent problem are actually related. If you take a function and find its derivative, and then take the integral of that derivative, you will get the original function you started with (up to a constant C)! This idea is called the Fundamental Theorem of Calculus, and is one of humanity’s great accomplishments, also one of my favourite theorems.
In my next post, I’ll talk more about how the Fundamental Theorem of Calculus works, and why it’s such a cool theorem!
For further reading, I recommend James Stewart’s Calculus textbook (I’m using the 8th edition).
Until next time!