My favourite theorem at the moment is the Fundamental Theorem of Calculus:
The Fundamental Theorem of Calculus (FTC)
Let f be the derivative of F. Then:
This theorem roughly says that integration and differentiation are inverses of each other. If you integrate the derivative of a function, then you return to the original function. Equivalently, if you differentiate an integral, you also return to the original function.
The theorem directly unites the two branches of calculus: integral calculus (the area problem) and differential calculus (the tangent problem), which is interesting enough on its own.
But why is it true?
You can find a formal proof of this equation in a typical calculus textbook. But I think there’s a more intuitive reason for why integrals and derivatives should be opposites.
Stick around to the end, where I connect this idea with Stokes’ Theorem which generalizes the Fundamental Theorem of Calculus to higher dimensions!
The key idea: a bunch of small changes add up to a big change.
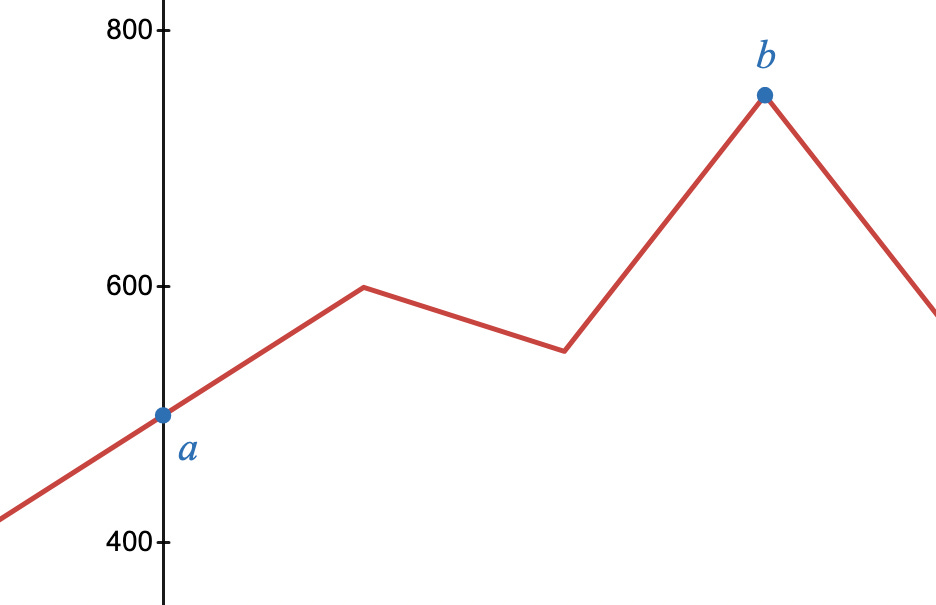
Example: Hiking Up A Mountain
Suppose you’re hiking up a mountain, from point a (x=0) to b (x=3). Naturally, the mountain has varying slopes as you ascend. The big question we want to answer is, what was the overall change in elevation from a to b?
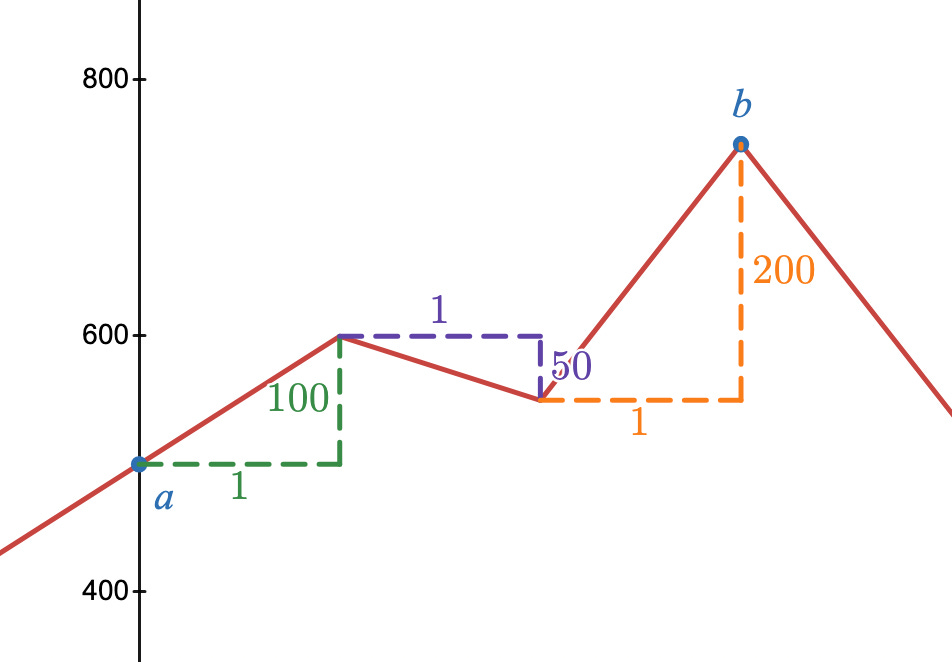
Some more info: Point a has an elevation of 500 metres above sea level. In the first hour of walking, you ascend 100m in elevation. In the second hour, you descend 50m, and in the third hour you ascend 200m, to finish the hike at point a, which is 750 metres above sea level.
What was the total change in elevation?
There are two ways to answer this.
First, you could just the elevation of point b minus point a, and 750 minus 500 is 250. That’s the right side of the FTC equation!
An alternative way is to just add up the elevation changes along the way. If you ascend 100m, descend 50m, and ascend another 200m, then that’s 100-50+200, which is 250m overall. That’s the left side of the FTC equation.
f(x) is the derivative of F(x). In other words, if F(x) is the elevation at time x, then f(x) is the change in elevation. Adding up all the incremental changes results in seeing the overall change!
That’s what an integral does: it’s just a sum. We’re adding up all the small changes.
Another way to write the FTC is this:
We replace f(x) with dF/dx, which is the same thing.
Even though this next part is technically illegal math, I like to imagine those dx’s cancelling each other out on the left side of the equation, so that the integral just looks like this:
It’s just adding up all the infinitesimal (vertical) changes from point a to b!
So, even if the elevation was changing with every step, as it does with a curve, all we’re doing is adding up all the positive elevation changes, subtracting all the changes where the slope was negative (descending), which results in the overall change.
To see how this works, let’s look at another example.
A Mathematical Example
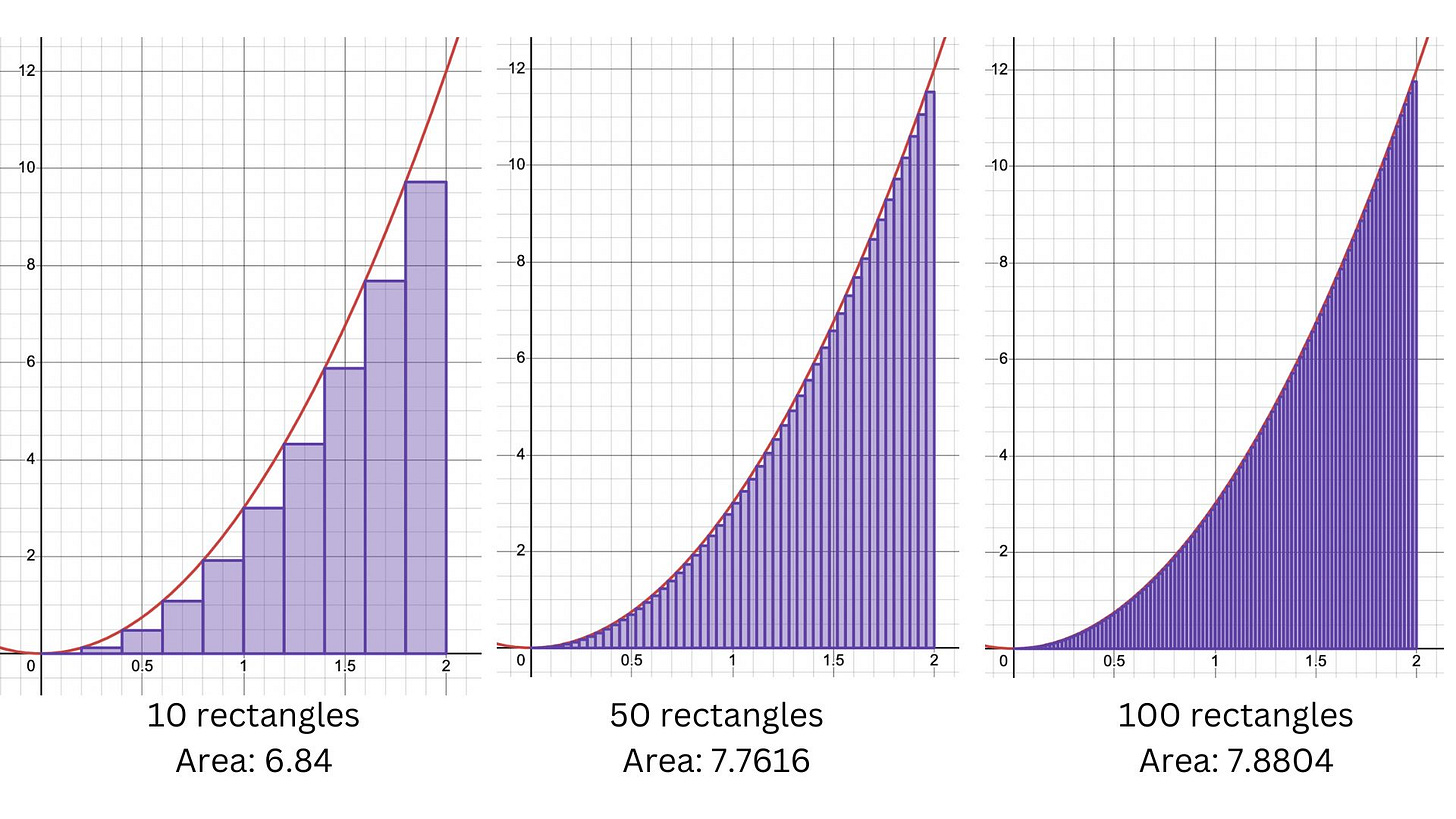
This is the area problem which I discussed in my last post. So it’s an integration problem! We want to approximate the area under this curve by partitioning [0,2] into subintervals of equal width, using the left endpoints as the heights of the rectangles.
We can split up [0,2] into n rectangles, and simply calculate the total area of all the rectangles.
The total area of 10 rectangles is 6.84. The area of 50 rectangles is about 7.76, and the area of 100 rectangles is about 7.88. Using 1000 rectangles, the area is just under 7.99.
The more rectangles we use, the closer we get to the true area under this curve, which is 8. 8 is the limit of this sequence of areas.
Enter, FTC!
The Fundamental Theorem of Calculus is the grand dame that cleans up this whole entire process. Instead of integrating f between a=0 and b=2 (the left side of the FTC equation), we can just use the right side of the equation which is a lot easier, and makes use of the antiderivative of f:
Now we just use the FTC:
Et voila, the answer is 8.
Generalized Stokes’ Theorem
The Fundamental Theorem of Calculus is actually just a special case of a more general theorem, which is Stokes’ Theorem (or the generalized Stokes’ Theorem):
ω is called a differential k-form, which is just a function. M is a manifold, like [0,2], or possible some higher dimensional smooth surface that you’re integrating over.
Put into words, this theorem states that the average of a derivative on the interior of a manifold (left side) is equal to the average of the original function on that manifold’s boundary (right side).
If you want to know the net change of a function, you can either look at the derivative on the interior, or the actual values of the function on the boundary.
The left side is equivalent to adding up all the little steps we took during our hike, or getting the area under 3x^2 by adding rectangles: we were adding up derivatives on the interior of the interval.
The right side is equivalent to finding the overall elevation change by just subtracting the elevation at b minus the elevation at a, or finding the area under 3x^2 by using the antiderivative, x^3 at the endpoints of the interval. In both cases, you’re only looking at the original function at its boundary.
(The boundary of the manifold [0,2] is the endpoints 0 and 2).
One More Example: Tracking Your Spending
How much money did you spend or earn last month?
You can find out by adding up all your deposits and withdrawals (or debits and credits) that took place during the month. AKA… the derivatives on the interior of the month.
Alternatively, you can find out how much your bank balance changes by simply taking the balance at the end of the month minus the balance at the beginning. AKA… the original function (or antiderivative) at the boundaries.
Final Thoughts
I have an easier time wrapping my head around Stokes’ Theorem when I think about the Fundamental Theorem of Calculus this way, so I hope this helped some of you!
Thank you as always for reading The Math Queen Digest. And extra thanks to my paid subscribers for making this work possible.