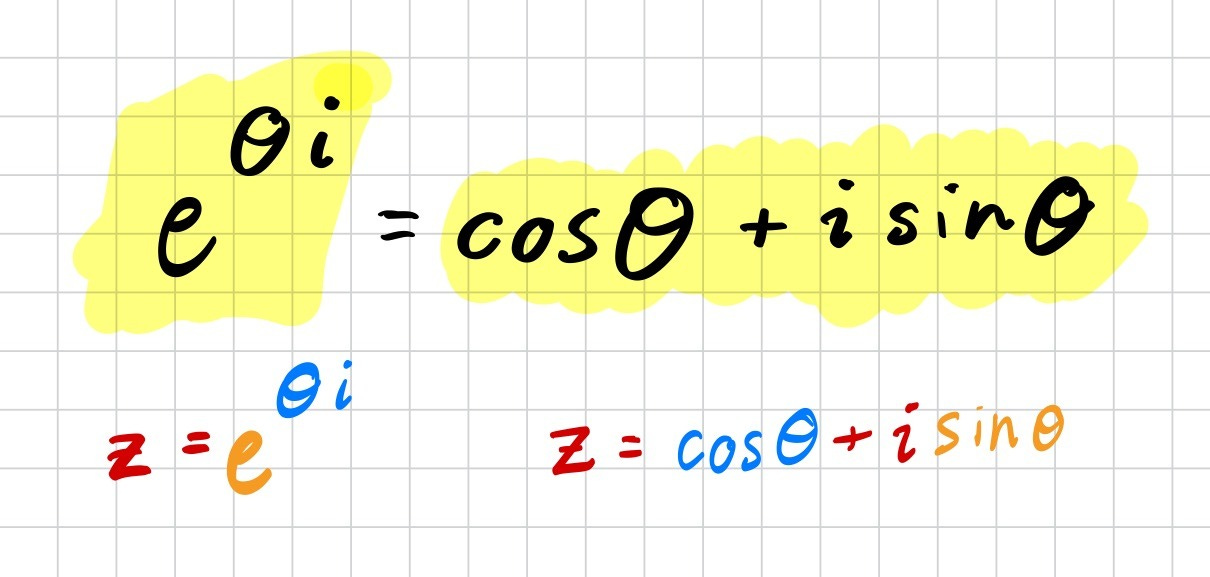Why e to the pi times i equals -1

Euler's Identity Explained

Hi everyone!

This post (along with my previous 4) is my personal attempt at making sense of Euler’s Identity without using the Taylor series.

\(e^{\pi i} = -1\)

A quick note before we get started. I received a response on my previous post saying that some equations had typos where they were missing an addition sign.

I appreciate messages about my errors, but in this case I think it wasn’t my fault. From my end, the typo seems to appear when I read my posts through the Substack mobile app on iOS. The equations appear correct when I read and edit these posts on desktop and through my email on mobile. Look!

On the left is how my LaTeX equations are appearing on the Substack mobile app. On the right is how they appear in my email (correctly, with the plus sign).

Obviously this is not acceptable! Substack’s customer support AI agent did not seem to understand my concern. I’m open to moving my blog to another platform which is more friendly to rendering math equations. Please shoot me a message (onlinekyne@gmail.com) if you have any thoughts on this!

Anyway, back to the topic at hand!

Euler’s Identity

In our last post, we took a look at Euler’s Identity and saw that the right hand side was related to representing complex numbers using trigonometry. The more general form of Euler’s identity looks like this:

\(e^{\theta i} = \cos{\theta} + i\sin{\theta}\)

Today, we’ll look at the left hand side and try to understand why e raised to the power of θ times i is a valid way of representing a complex number.

Complex Numbers as Rotations

Instead of thinking of a complex number as a sum of a real part and imaginary part, another way to view them is through their rotation around the origin, like like how i is associated with a rotation of π/2 radians, and -1 is associated with a rotation of π radians.

Is there a general way of writing the complex number z if all you know is its angle of rotation θ, without using trigonometry? What if we could represent rotating around the unit circle in some sort of continuous counter clockwise motion?

One fact we might explore is how multiplying complex numbers is the same as adding together their rotations.

For example, i has a rotation of π/2, so multiplying i by i gets us to an angle of π/2 + π/2 (indeed, i^2 = -1, which corresponds to a rotation of π radians or 180 degrees).

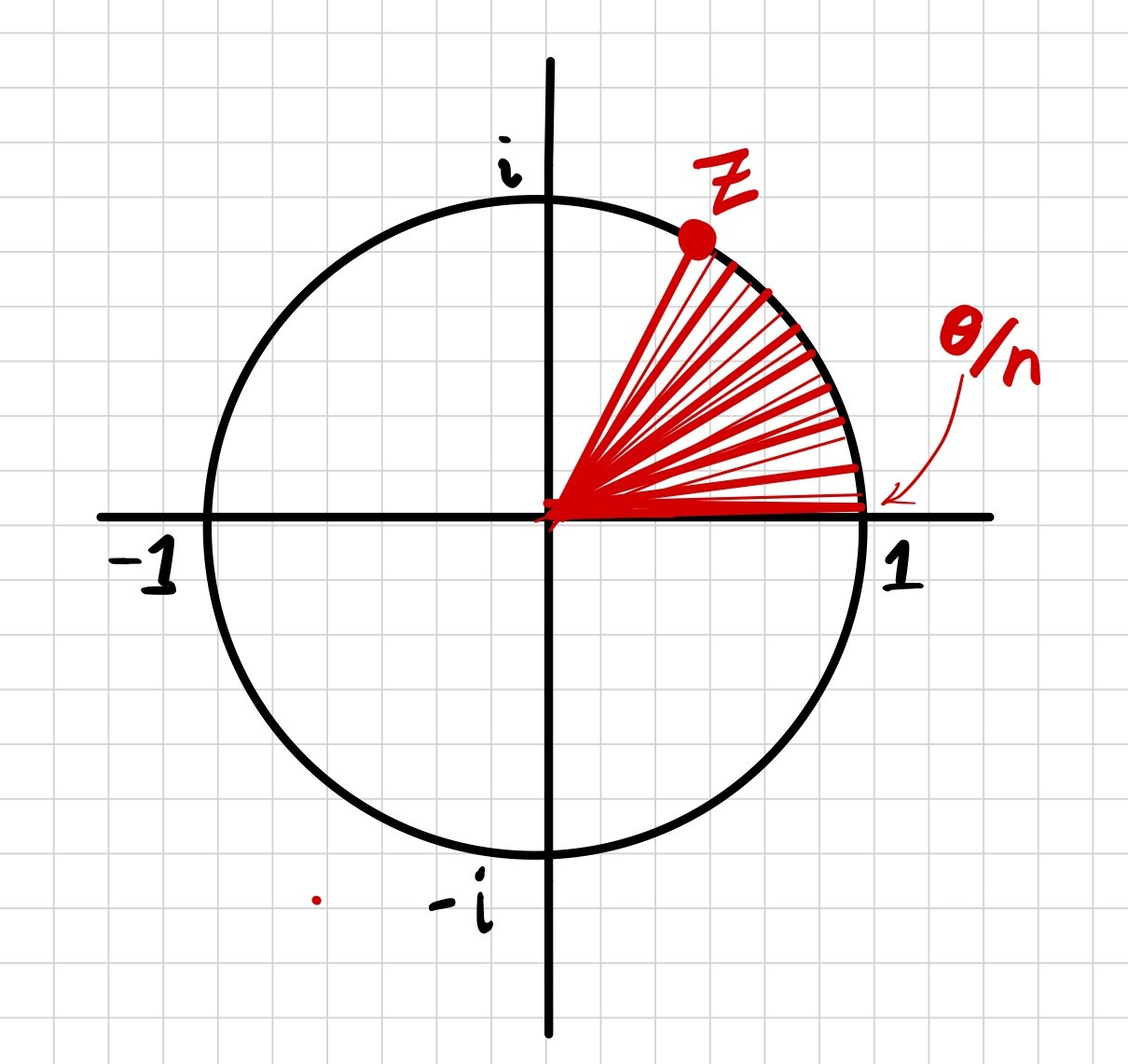
Suppose that z is a complex number on the unit circle, and it makes an angle of theta.

z on the unit circle with an angle of θ highlighted in red.

To reach z, we could take the complex number that’s located at the angle of θ/2 and just multiply it by itself.

Or we could use the complex number that’s at the angle of θ/10 and multiply it by itself 10 times.

What if we divided the angle θ into infinitely many slices? That is, divide it into n equal angles (θ/n) and take the limit as n approaches infinity. That might look something like this.

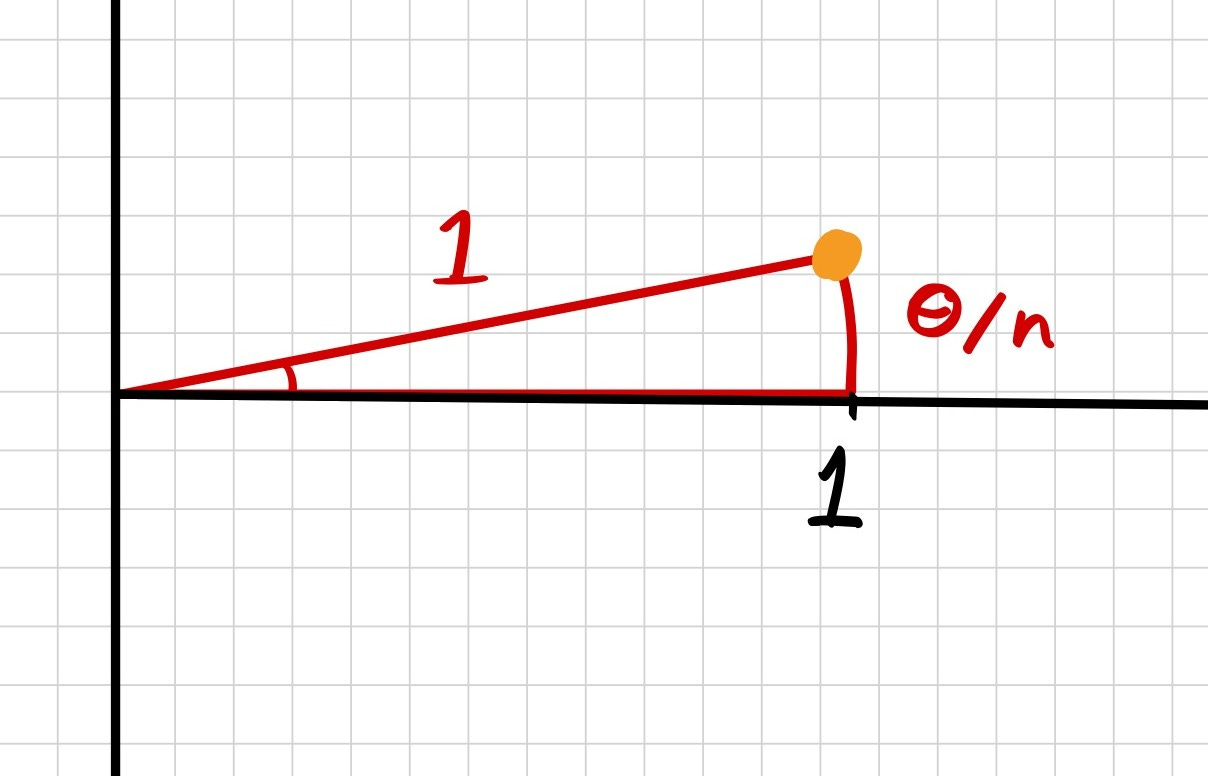
If we could write down that complex number which makes an angle of θ/n, we could just multiply it by itself a total of n times and thereby reach z. So let’s try zooming in on it so we can write down its real and imaginary part:

The complex number in question is represented by this orange dot on the unit circle

The complex number we want is that orange dot. When n is very large, then the angle is very close to 0, so the real part will be approximately 1. As for the imaginary part, the vertical height of the orange dot will be approximately close to the arc length, which is equal to θ/n.

Remember, since we’re using radians, the angle and the arc length are equivalent!

Thus the imaginary part will be (θ/n)i.

So the complex number we want to use looks something like this:

\(1 + \frac{\theta}{n} i\)

Now, to reach z, we want to multiply this thing by itself n times, and then take the limit as n approaches infinity:

\(z = \lim_{n \to \infty} \left(1 + \frac{\theta}{n} i \right)^n\)

If you are familiar with limits and with e, then you may recognize this as being reminiscent to the limit for e^x:

\(e^x = \lim_{n \to \infty} \left( 1 + \frac{x}{n} \right) ^n\)

And the proof is done, since we simply replaced x with θi:

\(z = e^{\theta i}\)

If you’re not familiar with e, here’s a Wikipedia article explaining how it’s connected to the limit above. I’ll do a dedicated blogpost about e another time! Just another mathematical thing named after Euler haha.

Now we have a way of expressing complex numbers in two ways: with rotations on one side, and with triangles on the other side! When we substitute θ with π, we get the famous identity:

\(e^{\pi i} = -1\)

Isn’t math fantastic?