Why Use Radians?
Exploring Euler's Identity
Hey everyone! Before we dive into today’s math topic, I wanted to update y’all that I’ve started posting YouTube videos again. I’m planning on posting vlogs on there about my day to day life (not necessarily about math or drag). In my newest video, I open up about my journey as a content creator and what I plan to do in the future. Watch it here and let me know what you think!
Now let’s chat about some math. Currently, I’m working on understanding complex numbers better, with a view to eventually explain the meaning behind this wonderful equation:
We’ll call this equation Euler’s Identity.
In this post, I’ll explain the right-hand side of Euler’s Identity (we’ll tackle the left side next week)!
In my last 3 blog posts, we went over some basic mechanics about how complex numbers work. We saw that they can be useful for representing rotations around the Cartesian plane.
Now the next step is to refresh our trigonometry knowledge. Trigonometry is the branch of math which deals with angles and triangles, and it’ll give us new tools for thinking about complex numbers and the rotations that they make.
If you’ve studied trigonometry before, you may recall converting between degrees and radians. In radians, the angles 45°, 60° and 90° are equivalent to π/4, π/3, and π/2.
When I first encountered them in school I found it kind of confusing and arbitrary. Why make trigonometry any more complicated than it needs to be? What’s wrong with our old-fashion degree system?
Once upon a time, people chose to split up a circle into 360 degrees. The reason behind the number 360 seems to be unknown. Maybe it’s because it’s approximately the number of days in a year, or perhaps we chose 360 because it has a lot of factors. You can split it up into halves, thirds, fourths, fifths, sixths, eighths, ninths, tenths, twelfths, and so on without needing to use any decimals.
For practical calculations, 360 is a convenient number. But it could be more convenient. Why not double it to 720 which has even more factors? Or why not a number like 1000 like most metric units?
There’s another number we could use which is much more natural to the circle, which is π!
Degrees vs Radians
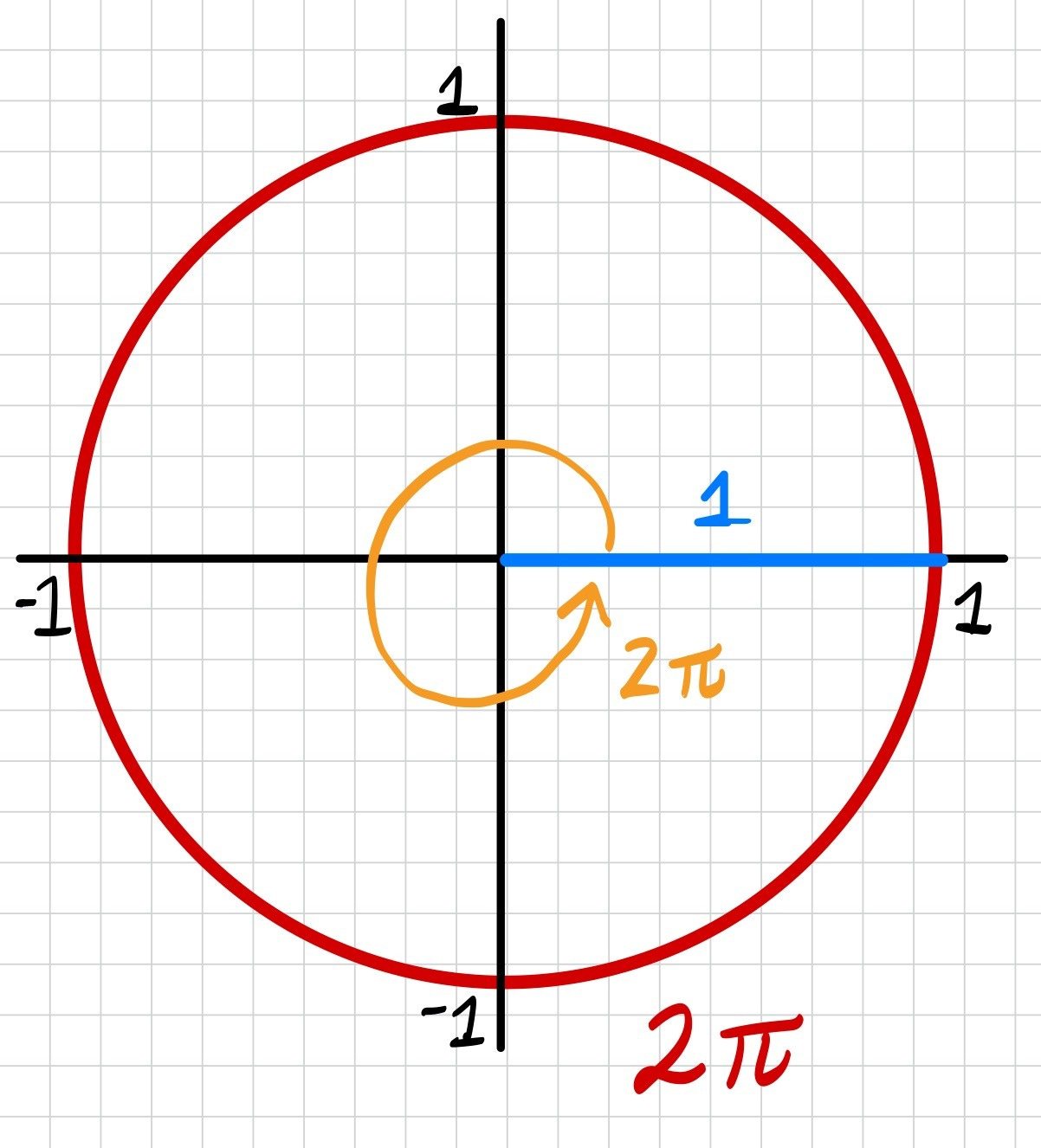
A circle with a radius of 1 will have a circumference of 2π.
In radians, a full rotation around the circle is simply 2π radians, instead of 360 degrees.
A half rotation is simply π radians (instead of 180 degrees), because the length around half of the circle is π units.

In radians, the angle of rotation is directly linked to the portion of the circle’s circumference that you’re tracing around (this is called the arclength).
In a sense, radians are more natural because they are based on divisions of the circle’s circumference rather than divisions of 360. This fact will be crucial when we prove the left hand side of Euler’s Identity next week!
Euler’s Identity
Now let’s see how radians and trigonometry fit into Euler’s Identity. This equation is actually a special case of a more general equation, which we’ll call Euler’s Formula:
This equation is giving us an equivalence between two ways to represent a complex number which lives on the unit circle. Let’s see how the right hand side does this.
Pick a complex number on the unit circle, and let’s call it z.
It has coordinates (x,y), where x and y are both real numbers. We can write z like this:
Now let’s draw a right angled triangle, and we’ll see that the hypotenuse is 1 (since this is the unit circle), and the other two sides are x and y.
Remembering trig class, we know that the cosine of θ is the adjacent side over the hypotenuse, which would be x over 1.
Thus cosθ = x. Similarly, sinθ = y.
Therefore…
Which explains the right side of Euler’s Formula!
To see how it could equal -1, simply plug in θ = π (AKA 180 degrees).
Since the cosine of π is -1 and the sine of π is 0, we have:
The righthand side of Euler’s formula is a way of representing complex numbers using their real part (cosθ) and imaginary part (i sinθ). This is also known as the rectangular form of a complex number.
Next time, we’ll see how the lefthand side of Euler’s formula can also represent the same complex number but through the lens of a continuous rotation around the unit circle, and we’ll see that Euler’s number (e) has something to do with it!
Thanks for reading!