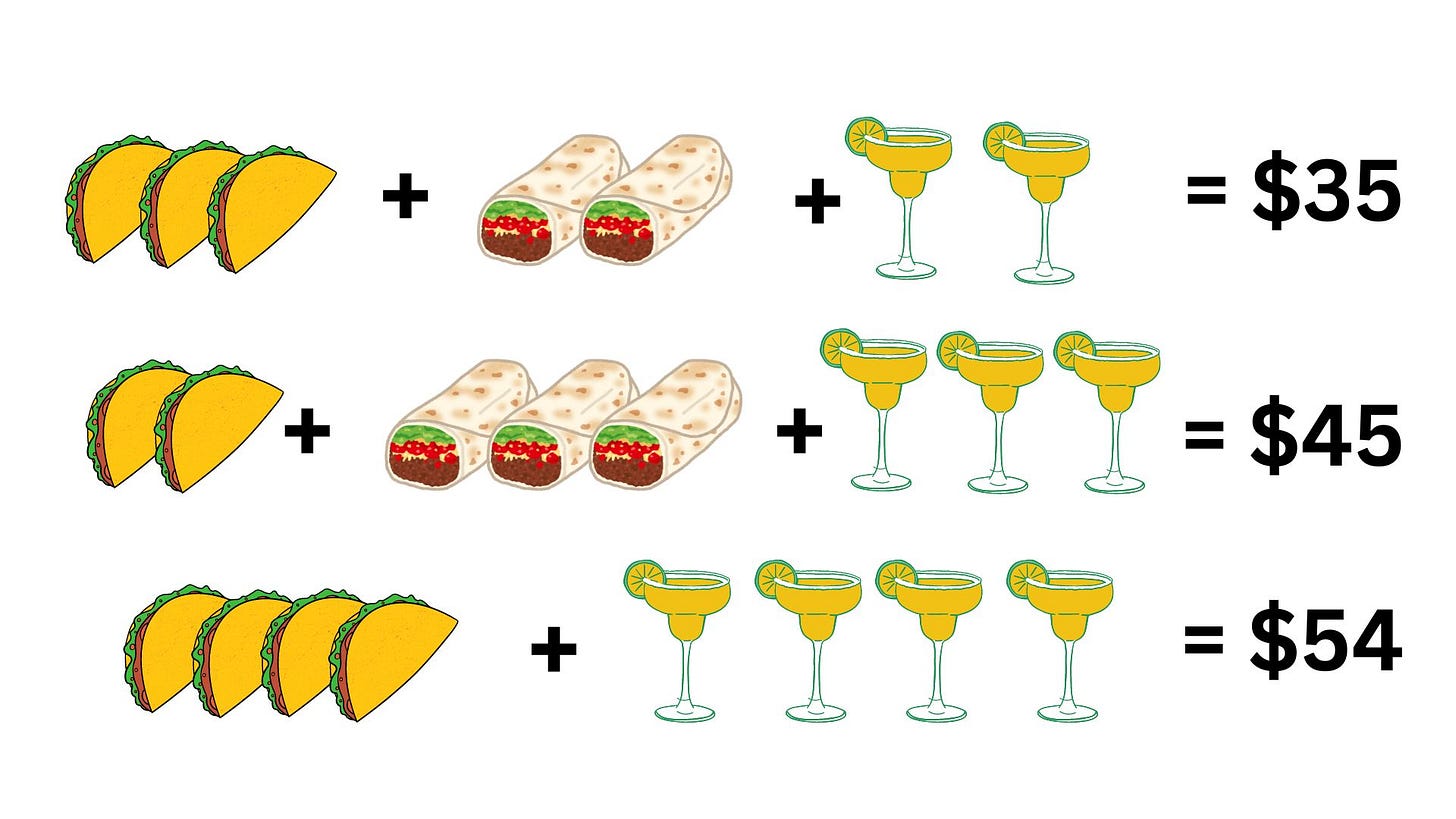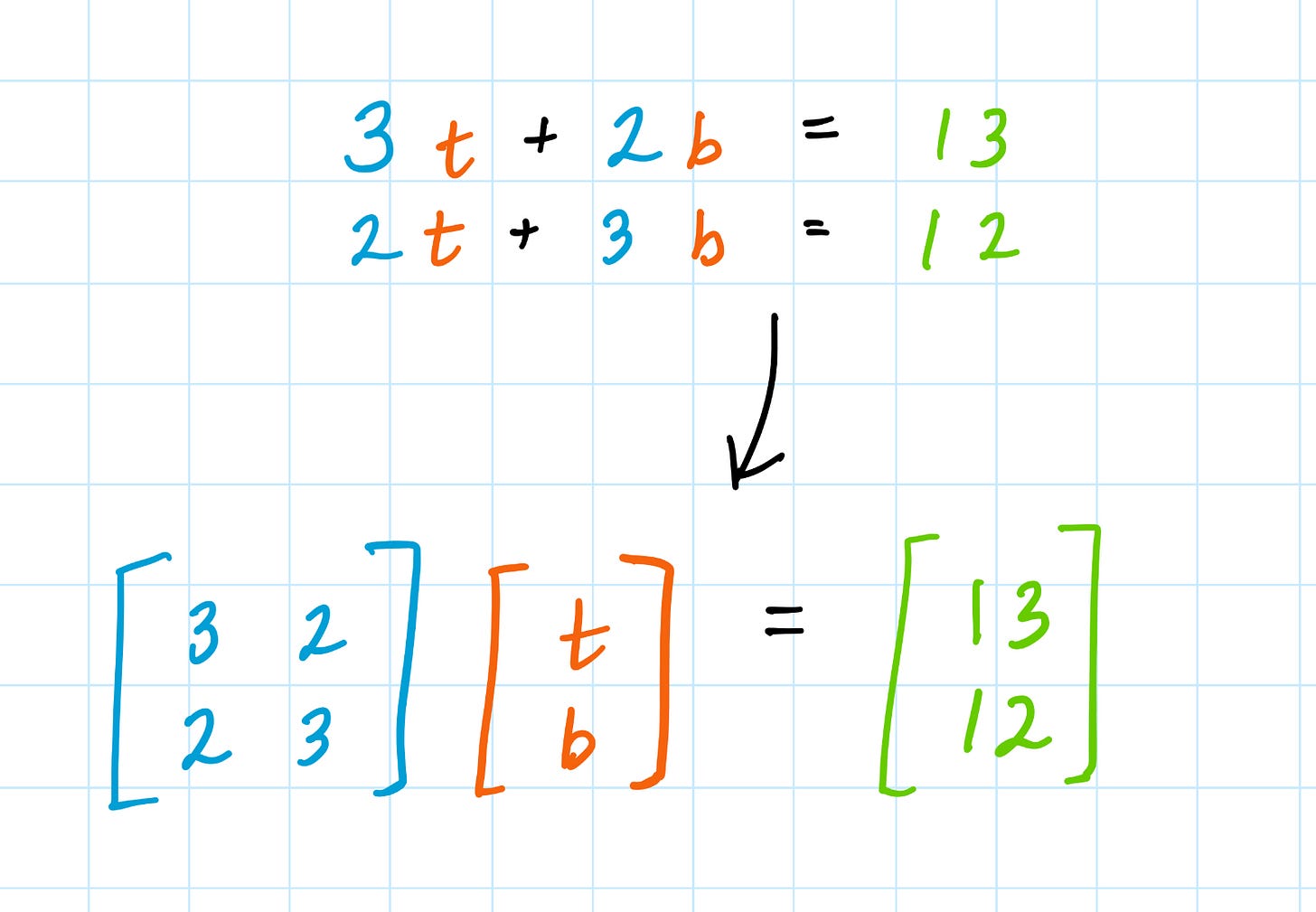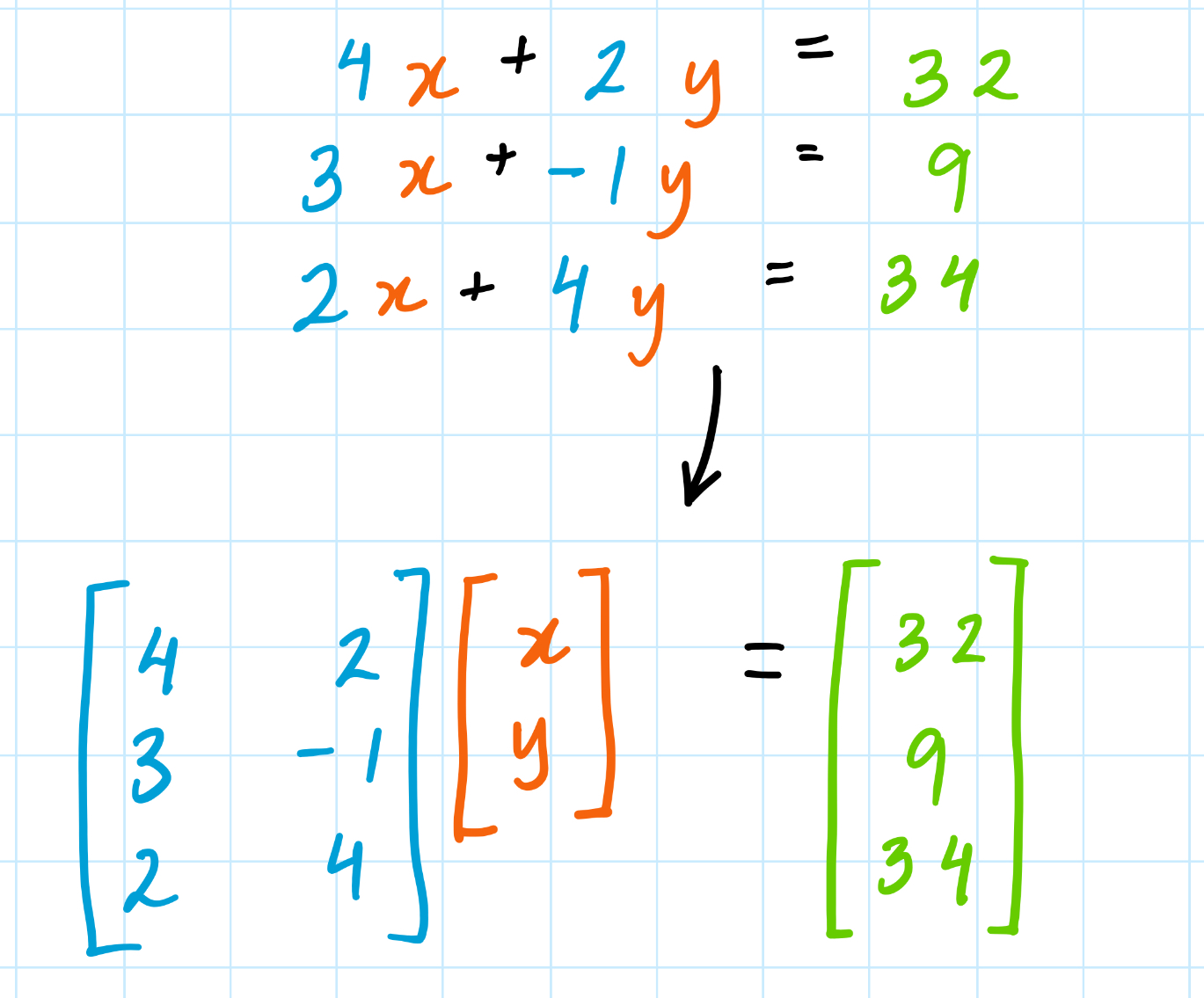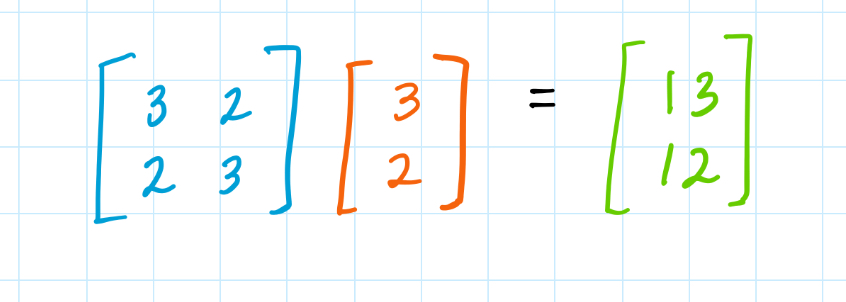Hello everyone! This week’s post is part 4 of my series on linear algebra. For parts 1-3, see below:
This week, we’re meeting the star of linear algebra, which is the matrix.
The way I first learned about matrices in high school was that a matrix was a table of numbers:
And I had to learn all these rules for matrix-vector multiplication, dot products, cross products, reduced-row-echelon form, blah blah blah, all without really understanding what a matrix really is.
Of course, all that stuff is important to learn, just like a musician should learn how to play scales and a writer should learn about grammar. But I want to spend some time reflecting on the big picture idea of what a matrix represents, and why it’s worth thinking about at all.
Though a bit of an exaggeration, it can be said that a mathematical problem can be solved only if it can be reduced to a calculation in linear algebra. And a calculation in linear algebra will reduce ultimately to solving a system of linear equations, which in turn comes down to the manipulation of matrices.
- Thomas A. Garrity
Matrices As Systems of Equations
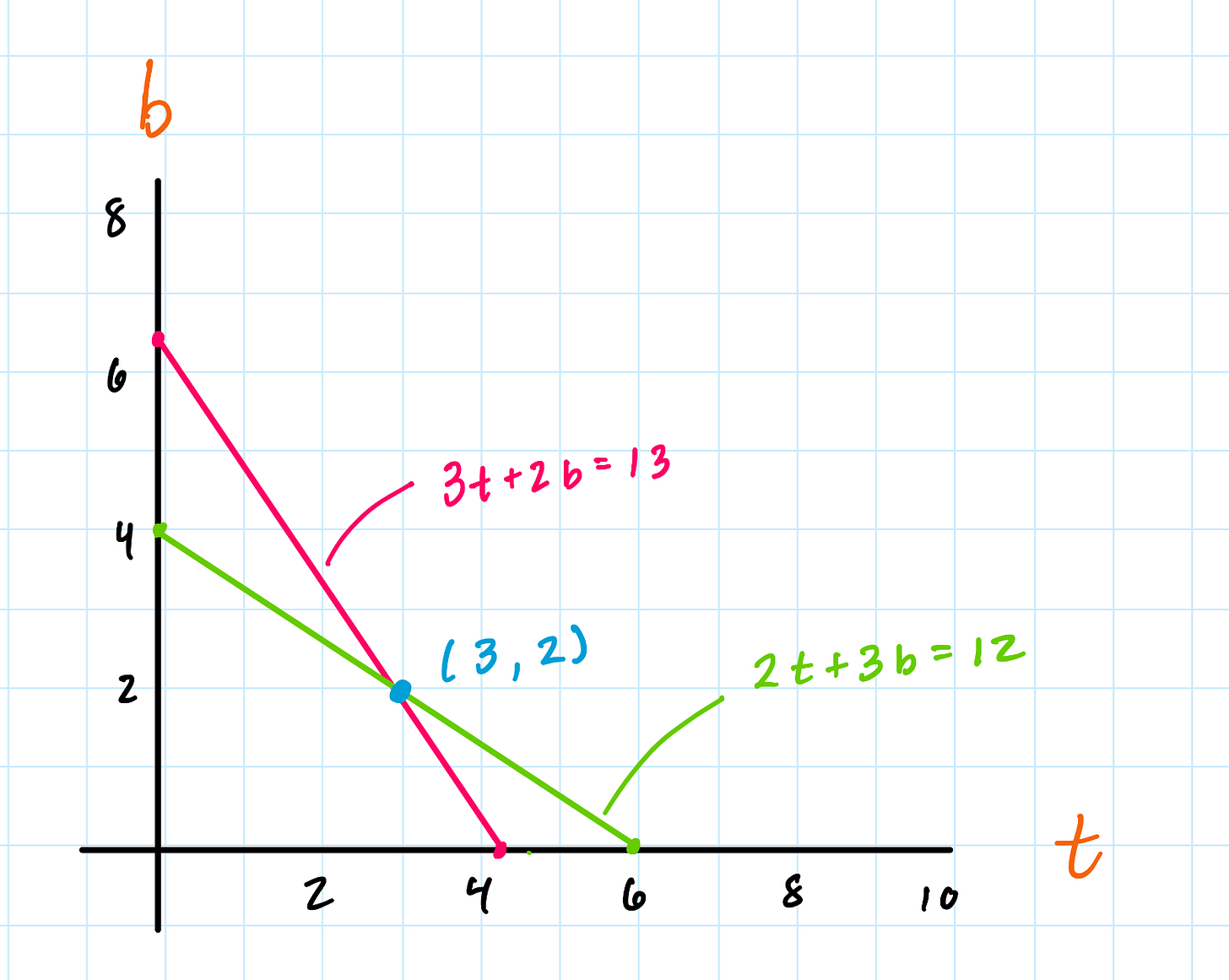
You’re hungry so you decide to go to a Mexican restaurant, and you buy 3 tacos and 2 burritos for $13. The next day, you switch it up and get 2 tacos and 3 burritos, which costs $12. What is the individual price per taco and per burrito?
We can model this using a system of equations:
Where t is the price for 1 taco and b is the price for 1 burrito.
We have two unknown variables t and b, and two equations. Each equation can be plotted as a line, with our two axes being t and b.
The lines intersect at (3,2), meaning that t = $3 and b = $2 satisfies both equations.
What if you had a system of equations involving 3 unknowns and 3 equations?
Solving this system would correspond to finding the intersection point between 3 planes in 3 dimensions.
Of course, we can also solve a system of 4 equations with 4 unknowns, which would correspond to finding the intersection between 4 hyperplanes, but unfortunately Desmos doesn’t support 4D graphs yet.
To make things simpler, we can represent all the important information about a system of linear equations using something called a matrix.
Remember how a vector is a list of numbers? A matrix is just like a list of vectors.
Multiplying by a matrix just means you’re unfolding this notation back into the system of equations. The top row of the matrix gets “multiplied” by the column vector (t, b) to make the equation 3t + 2b = 13, and then the bottom row gets “multiplied” by the same column vector to make the equation 2t + 3b = 12.
Matrices don’t have to be square, for instance this 3x2 matrix represents a system of 3 equations with two unknowns.
In turn, a solution to this system would be an intersection between 3 lines on a 2D plane.
But it’s also possible for 3 lines to have no common intersection at all. If we slightly alter one of these equations, we can turn this into a system that has no solutions, since there’s no point (x,y) that lives on all three lines.
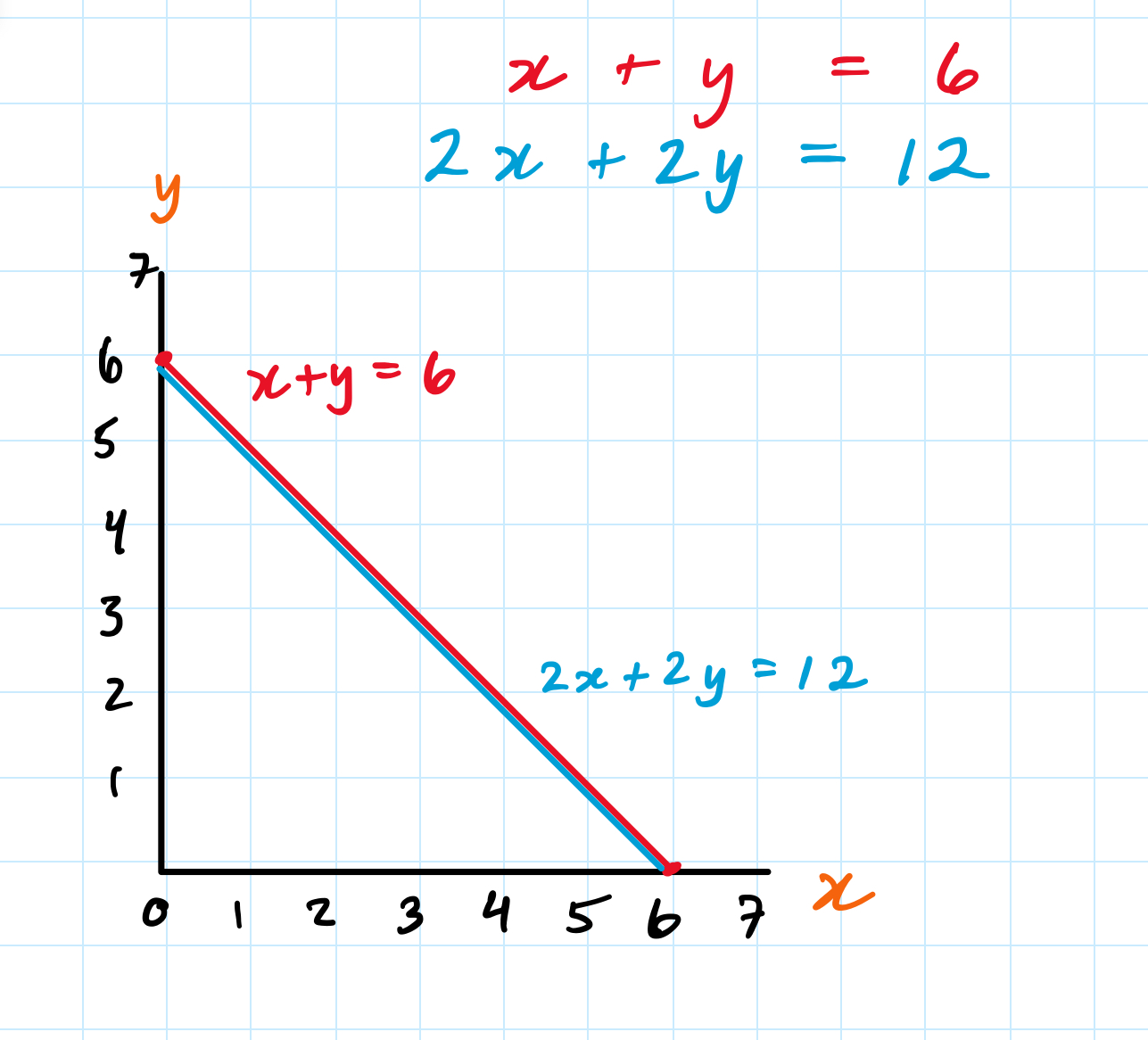
It’s also possible for a system to have infinitely many solutions! Consider this system of 2 equations. Since one equation is a scalar multiple of the other, they really just represent the same line. Thus there are infinitely many points (x,y) which satisfy both equations.
As a matrix, the equations x+y and 2x+2y can be represented as:
The reason this system has no unique solution (instead, it has infinitely many) is related to the fact that the columns of the matrix (or, the rows) are not linearly independent. (See my previous post on basis vectors and pokemon for a refresher on what linear independence means.)
A system of linear equations either has 0 solutions, 1 solution, or infinitely many solutions.
One of the main problems in linear algebra asks whether we can look at a matrix and judge immediately whether it represents a system of equations that has a unique solution.
The Inverse Matrix Theorem in linear algebra gives us multiple equivalent ways to check whether a unique solution exists!
Matrices as Linear Transformations
Just like vectors can be both lists of numbers and arrows in space, a matrix can be viewed as both:
A system of linear equations, and
A function that transforms a vector.
Lets revisit our previous example of the matrix (in blue) which represented buying 3 tacos and 2 burritos, and then 2 tacos and 3 burritos.
Viewed as a function, the matrix takes the orange vector [3,2] as its input, and outputs the green vector [13,12]. We can think of the matrix as the transformation from the orange vector to the green vector:
Here’s another visualization of what the matrix is doing to the vector space:
(Here’s how I created this video!)
Now you should have a better understanding of how matrices can operate as representations of both systems of linear equations, as well as linear transformations of vectors.
Next time, we’ll put everything together and learn about other matrix properties (determinant, eigenvectors, kernel) that can give us useful insight about both the system of equations as well as what the linear transformation is doing!