Why Is It Called LINEAR Algebra?

Defining Linearity

You hear the word “linear” a lot in math. There’s linear algebra, linear transformations, linear equations, linear combinations, linear independence, linear regression!

What’s the deal with linearity?

In this post:

1. Definition: Linear Functions

2. Examples

3. Linearity in Higher Dimensions

4. Affine Functions

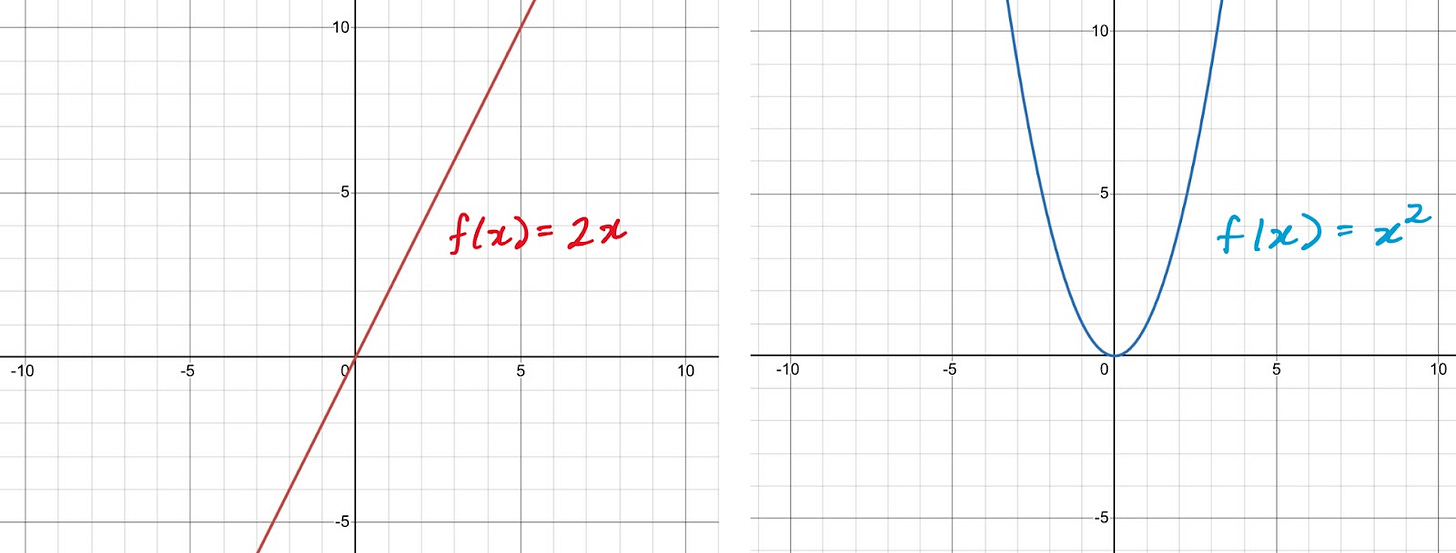
When you see the word “linear”, you might think about a straight line, like the difference between y = 2x and y = x^2.

But there’s more to it than that. In this post, we’ll see how the concept of linearity can be generalized beyond straight lines, and refer to any operation that’s compatible with addition and scalar multiplication. This definition will work even in higher dimensions, with vector-valued functions.

1. Definition: Linear Functions

Mathematically, a function f is linear if given any two inputs x and y, and any real number a, we have:

\(f(x+y) = f(x) + f(y)\)

and

\(f(ax) = a \cdot f(x)\)

In simple terms, a function is “linear” if changes in the function’s input cause proportional changes in the function’s output:

• If I double the input of a function, does that correspond to doubling the output?

• If I add up the inputs of a function, does that correspond to adding up the outputs?

And, we can replace “double” with multiplying by any scalar multiple a, like tripling (a = 3), halving (a = 0.5), or even applying negative numbers (a = -4).

2. Examples

A square’s side length vs area (non linear)

• Doubling a square’s side length does NOT correspond to doubling its area

• The area of a square with side length 1 plus the area of a square with side length 2 is NOT the same as the area of a square with side length (1+2)

Hence, this is not a linear relationship.

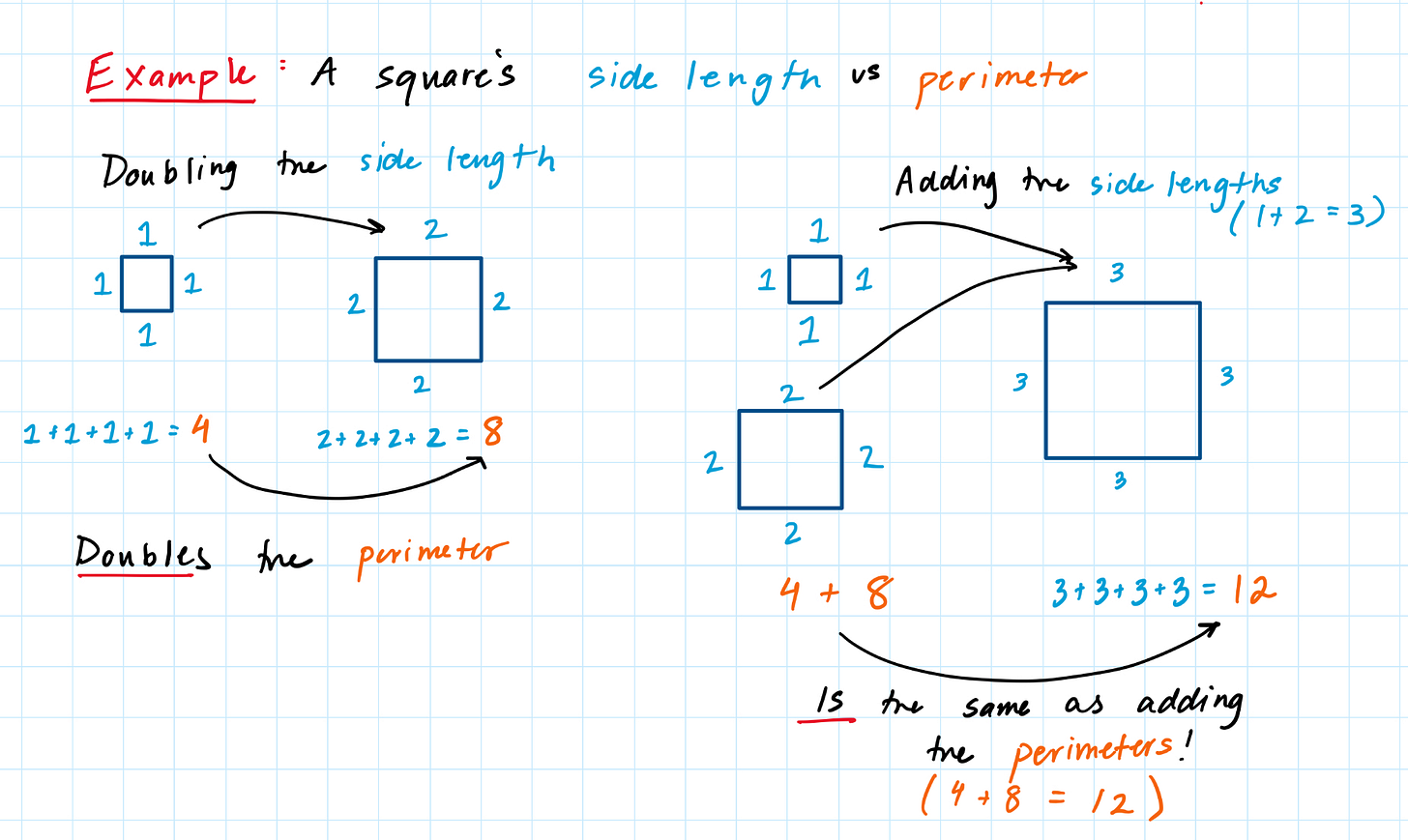
A square’s side length vs perimeter (linear)

• Doubling a square’s side length does correspond to doubling its perimeter

• The perimeter of a square with side length 1 plus the perimeter of a square with side length 2 is the same as the perimeter of a square with side length (1+2)

Hence, this is a linear relationship!

A 50% discount (linear)

Say you work at a store where you have an employee discount of 50%, and you want to buy 2 handbags, which cost $400 and $600. Is it better to split them up into 2 transactions and use your discount on each bag separately, or should you just buy them at the same time and use your discount on the total? Does it make a difference?

If you split it up into two transactions and use your discount separately, the prices would go from $400 and $600 down to  $200 and $300, for a total of $500. 

\(0.5(400) + 0.5(600) = 200 + 300 = 500 \)

If you bought them in one transaction, the total would be $1000 before your 50% discount, and $500 after. 

\(0.5(400 + 600) = 0.5(1000) = 500\)

It’s the same price whether you do two transactions or one!

In math-terms, your employee discount is a function that preserves addition, since using it before adding the bags together is the same thing as using it after adding the bags together.

What if you were also allowed to combine your employee discount with a 10%-off coupon? Is it better to use your discount before or after the coupon? 

If you use your discount before the coupon, the $400 bag would be discounted down to $200, and then after another 10%, the $200 goes down to $180. 

\(0.9(0.5 * 400) = 0.9(200) = 180 \)

If you use your discount after the coupon, then the $400 bag would go down to $360, and then your discount would cut it by 50%, down to $180. Again, the same price!

\(0.5(0.9*400) = 0.5(360) = 180\)

We can also say that the employee discount preserves scalar multiplication.

Hence, this relationship between the price of a bag before and after a 50% discount is a linear relationship!

A square root discount (non linear)

Say your employee discount was actually a square root function, so you only pay the square root of the original price.

If you split it up into two transactions, then you’ll pay the square root of $400 plus the square root of $600, which is $44.49.

\(\sqrt{400} + \sqrt{600} = 20 + 24.49 = 44.49\)

If you bought them in one transaction, you’d only pay the square root of the total (1000), which is only $31.62. It makes a difference now!

\(\sqrt{400+600} = \sqrt{1000} = 31.69\)

It also makes a difference whether you apply it before or after a scalar multiplication.

If you use your discount before the coupon, then you get 10% off of the square root of $400.

\(0.9\sqrt{400} = 0.9(20) = 18\)

If you use your discount after the coupon, then you pay the square root of 10% off of $400.

\(\sqrt{0.9*400} = \sqrt{360} = 18.97\)

When your employee discount was simply 50%, it didn’t matter whether you split up the transactions or what order you used your coupon, but if your discount was a square root function, there’s a difference. Thus this is a non linear relationship!

We’ve now seen two examples of linear relationships which have nothing to do with straight lines! The perimeter of a square and a 50% employee discount.

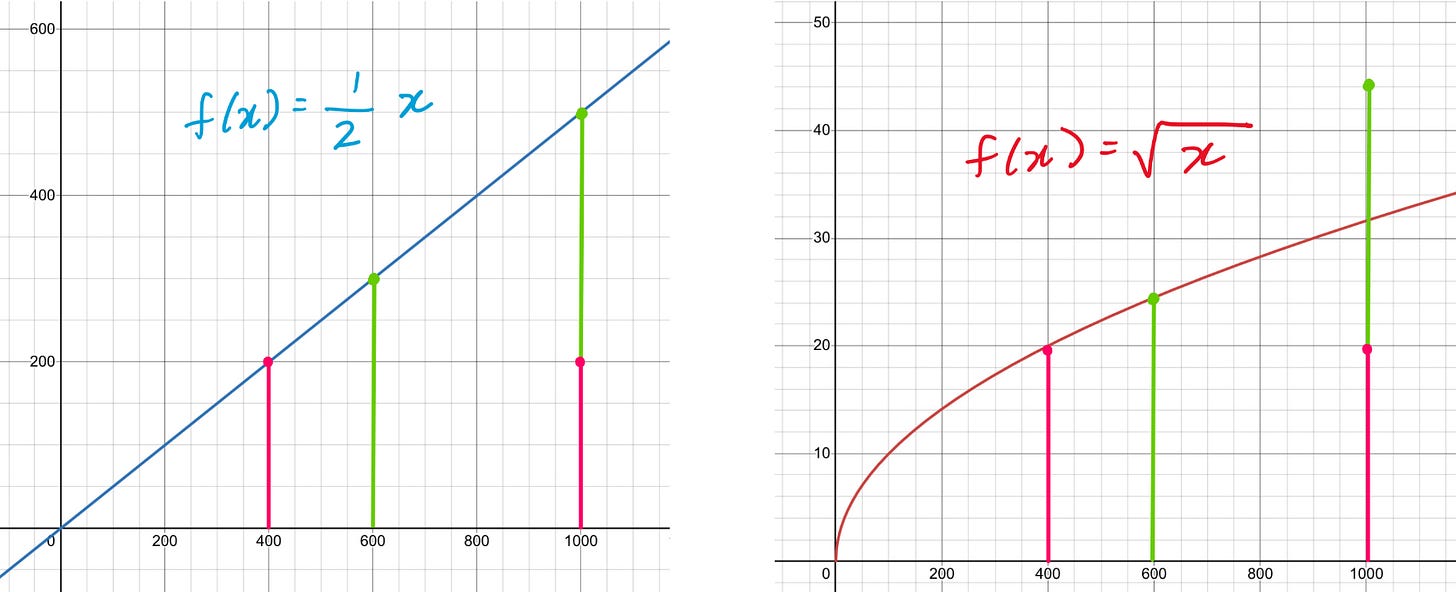
We can relate this back to straight lines by using graphs. On the left, the function representing a 50% discount, which is linear and works nicely with addition. On the right is the graph representing the square root function, which does not preserve addition.

The square root function is only one example of a nonlinear function. Some other examples are the square function, the reciprocal function, and the exponential function. Not only are these graphs not straight lines, but they also fail to preserve addition and scalar multiplication:

\((a+b)^2 \neq a^2 + b^2 \text{ and } (\lambda a)^2 \neq \lambda(a)^2\)

\(\frac{1}{a+b} \neq \frac{1}{a} + \frac{1}{b} \text{ and } \frac{1}{\lambda a} \neq \lambda\frac{1}{a} \)

\(2^{a+b} \neq 2^a + 2^b \text{ and } 2^{\lambda a} \neq \lambda 2^a\)

This is what we mean by linearity “preserving” addition and scalar multiplication.

It also relates to the idea of proportionality between two variables. In my post on linear regression, we explored whether a drag queen’s performance length was proportional to the amount of tips they collected during the performance. If we “doubled” the performance time, did that correspond to “doubling” the amount of tips we get?

3. Linearity in Higher Dimensions

So far, we’ve only talked about linear functions with one variable. Let’s see how it works with multivariate functions.

Let f be a vector-valued function in R2, defined as follows:

\(f \left( \begin{bmatrix} x \\ y \end{bmatrix} \right) = \begin{bmatrix} 2x \\ y \end{bmatrix} \)

So f takes a 2-dimensional vector (x,y) and just doubles the x-coordinate. We will see that this is a linear function:

\(f ( \begin{bmatrix} x_1 \\ y_1 \end{bmatrix} + \begin{bmatrix} x_2 \\ y_2 \end{bmatrix}) = f ( \begin{bmatrix} x_1 + x_2 \\ y_1 + y_2 \end{bmatrix}) = \begin{bmatrix} 2(x_1 + x_2) \\ y_1 + y_2 \end{bmatrix} = \begin{bmatrix} 2x_1 + 2x_2 \\ y_1 + y_2 \end{bmatrix} = f ( \begin{bmatrix} x_1 \\ y_1 \end{bmatrix}) + f(\begin{bmatrix} x_2 \\ y_2 \end{bmatrix}) \)

So f preserves addition.

\(f ( \lambda \begin{bmatrix} x_1 \\ y_1 \end{bmatrix}) = f ( \begin{bmatrix} \lambda x_1 \\ \lambda y_1 \end{bmatrix}) = \begin{bmatrix} 2 \lambda x_1 \\ \lambda y_1 \end{bmatrix} = \lambda \begin{bmatrix} 2 x_1 \\ y_1 \end{bmatrix} = \lambda f (\begin{bmatrix} x_1 \\ y_1 \end{bmatrix}) \)

And f preserves scalar multiplication, where

\(\lambda \text{ is a real number } \mathbb{R}\)

This function that doubles all the x-coordinates is equivalent to stretching all the vectors in R2 horizontally, something we looked at in the previous post about vectors!

The effect of doubling all the x-coordinates of vectors in the 2-D plane

The reason we call it linear algebra is because we’re interested in the properties of linear functions, AKA linear transformations. Horizontal stretch is one example, but so are rotations, reflections, and shears! Linear functions are everywhere. It’s been said that almost any math problem can be solved if it can be reduced down to a problem in linear algebra.

4. Affine Functions

A little footnote before I go. You might notice that the general equation of a straight line y=mx+b technically breaks our definition of a linear function.

Let’s see the function f(x) = 2x+1, which is a straight line:

The function y=2x+1

This function does not preserve addition, since f(a+b) is not equal to f(a) + f(b)

\(f(a+b) = 2(a+b) + 1 = 2a + 2b + 1\)

\(f(a) + f(b) = (2a+1) + (2b+1) = 2a + 2b + 2\)

It also fails to preserve scalar multiplication. Tripling the input doesn’t give us the same result as tripling the output.

\(f(3x) = 2(3x) + 1 = 6x + 1\)

\(3f(x) = 3(2x+1) = 6x+6\)

Technically, the general equation of a straight line y=mx+b is not a linear function, even though it looks like one. We call it an affine function.

Affine functions are linear functions plus a translation.

A key element of linear functions is that they must map 0 to 0. So they have to go through the origin.

Why? Well, if we want to preserve scalar multiplication, that means we should be able to factor out any scalar multiples in the input and apply it directly to the output, meaning that an input of 0 is the same as multiplying the entire result by 0. Hence, the function has to map 0 to 0.

Linear maps and affine maps both preserve straight lines when applied to vector spaces, but there’s a subtle difference.

Luckily, every affine function can be turned into a linear function by moving the constant term to the other side of the equation:

\(2x + 1 = 0 \implies 2x = -1\)

On the right side, we have the linear function 2x by itself!

Now you should have a solid understanding of what linearity means, and how it can be generalized to natural relationships and even higher dimensions! In the next post, we’ll continue our journey through linear algebra, and use linear combinations to create vector spaces in different dimensions.

As always, feel free to shoot me a message or email if you have any questions or spot any errors here. See you next time!